解:(1)∵AD∥BC,CE=AD,
∴四边形ACED为平行四边形
∴DE∥AC,DE=AC
∵四边形ABCD是等腰梯形,
∴AC=BD,
∴BD=DE,
∴∠E=∠DBE,
∵AC⊥BD,AC∥DE,
∴DE⊥BD,
∴∠BDE=90°,
∴∠E=45°
∵DE∥AC,
∴∠E+∠ACE=180°,
∴∠ACE=135°
(2)∵AD=CE,
∴BE=BC+CE=BC+AD=10cm,
∴Rt△BDE中,由勾股定理得:BD
2+DE
2=BE
2,
又∵BD=DE,
∴BD
2=50,
∴S
△BDE=
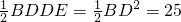
cm
2.
分析:(1)先根据AD∥BC,CE=AD判断出四边形ACED为平行四边形,故可得出DE∥AC,DE=AC,由四边形ABCD是等腰梯形可知AC=BD,BD=DE,∠E=∠DBE,再根据AC⊥BD,AC∥DE可判断出△BDE是等腰直角三角形,故∠E=45°,再由平行线的性质即可得出结论;
(2)由AD=CE可知BE=BC+CE=BC+AD=10cm,在Rt△BDE中,由勾股定理得:BD
2+DE
2=BE
2,由BD=DE,可知BD
2=50,再由三角形的面积公式即可得出结论.
点评:本题考查的是等腰梯形的性质及等腰直角三角形的判定定理,熟知等腰梯形的两底角相等是解答此题的关键.

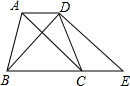 如图,已知四边形ABCD是等腰梯形,AD∥BC,对角线AC⊥BD,延长BC至E点,使CE=AD,连接DE.
如图,已知四边形ABCD是等腰梯形,AD∥BC,对角线AC⊥BD,延长BC至E点,使CE=AD,连接DE.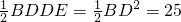 cm2.
cm2.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案
 的延长线分别交于点F、E,且
的延长线分别交于点F、E,且
