
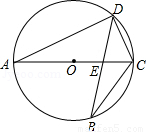
如图,AC是⊙O的直径,弦BD交AC于点E.
(1)求证:△ADE∽△BCE;
(2)如果AD2=AE•AC,求证:CD=CB.
证明:

(1)∵∠A与∠B都是弧 所对的圆周角,
∴∠A=∠B,
所对的圆周角,
∴∠A=∠B,
又∵∠AED =∠BEC,∴△ADE∽△BCE。
(2)∵AD2=AE•AC,∴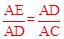 。
。
又∵∠A=∠A,∴△ADE∽△ACD。∴∠AED=∠ADC。
又∵AC是⊙O的直径,∴∠ADC=90°。∴∠AED=90°。
∴直径AC⊥BD,∴CD=CB。
【解析】圆周角定理,对顶角的性质,相似三角形的判定和性质,线段垂直平分线上点的性质。
(1)由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠A=∠B,又由对顶角相等,可证得:△ADE∽△BCE。
(2)由AD2=AE•AC,可得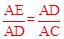 ,又由∠A是公共角,可证得△ADE∽△ACD,又由AC是⊙O的直径,可求得AC⊥BD,由线段垂直平分线上的点到线段两端距离相等的性质可证得CD=CB。
,又由∠A是公共角,可证得△ADE∽△ACD,又由AC是⊙O的直径,可求得AC⊥BD,由线段垂直平分线上的点到线段两端距离相等的性质可证得CD=CB。


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
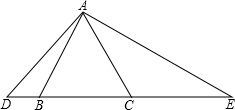 如图,△ABC是一个边长为2的等边三角形,D、E都在直线BC上,并且∠DAE=120°
如图,△ABC是一个边长为2的等边三角形,D、E都在直线BC上,并且∠DAE=120°查看答案和解析>>
科目:初中数学 来源: 题型:
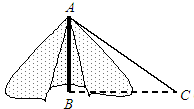 在“汶川”地震后人们积极开展自救.如图,这是小明家搭建的简易帐篷,小明准备从帐篷竖直的支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷.若地面固定点C到帐篷支撑竿底部B的距离是4米,∠ACB=30°,求支撑竿AB的长和绳子AC的长.(结果保留根号).
在“汶川”地震后人们积极开展自救.如图,这是小明家搭建的简易帐篷,小明准备从帐篷竖直的支撑竿AB的顶部A向地面拉一根绳子AC固定帐篷.若地面固定点C到帐篷支撑竿底部B的距离是4米,∠ACB=30°,求支撑竿AB的长和绳子AC的长.(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:
 某市的跨江斜拉大桥建成通车,如图,BC是水平桥面,AD是竖直桥墩,按工程设计的要求,斜拉的钢线AB、AC应相等,请你用学过的知识来检验AB、AC的长度是相等的,写出你的检验方法步骤,并简要说明理由.(检验工具为刻度尺、测角仪;检验时,人只能站在桥面上)
某市的跨江斜拉大桥建成通车,如图,BC是水平桥面,AD是竖直桥墩,按工程设计的要求,斜拉的钢线AB、AC应相等,请你用学过的知识来检验AB、AC的长度是相等的,写出你的检验方法步骤,并简要说明理由.(检验工具为刻度尺、测角仪;检验时,人只能站在桥面上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2008年江苏省南通市如东县马塘中学中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com