练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16、如图所示，点A、B表示两个村庄，直线MN表示一条水渠，现要铺设水管，把水渠里的水引到两个村庄，应怎样设计铺设路线，才能使铺设的水管最短？（要求在图上画出铺设的线路示意图，并简要说明理由）
    分析：作点A关于直线MN的对称点A′，连接A′B交直线MN于P，则点P即为引水的位置．
    解答：解：（1）作点A关于直线MN的对称点A′，连接A′B交直线MN于P，
    则点P即为引水的位置，此时，PA+PB的长度之和最短，即所铺设水管最短．
    理由：两点之间，线段最短．
    点评：此题主要考查点的对称问题及两点间直线最短，让学生学会简单的作图，比较简单．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上，分别连接BD、BF、FD，得到△BFD．
    （1）在图1-图3中，若正方形CEFG的边长分别为1、3、4，且正方形ABCD的边长均为3，请通过计算填写下表：
    正方形CEFG的边长  1   3  4
    △BFD的面积      
    （2）若正方形CEFG的边长为a，正方形ABCD的边长为b，猜想S△BFD的大小，并结合图3证明你的猜想．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    请把下列每对数在数轴上所对应的两点的距离写在横线上：
    （1）①3与2
    1
    1
    ；  3与-2
    5
    5
    ；
    ③-4与-4
    1
    2
    1
    2
    1
    2
    ；  ④-3
    1
    2
    与2
    1
    2
    6
    6
    ；
    你能发现求出距离与这两个数的差有什么关系吗？如果有一对数为a，b，则a，b两数所对应的两
    点之间的距离可表示为
    a-b
    a-b
    ．
    （2）如图所示，点A、B所代表的数分别为1，-2，在数轴上画出与A、B两点的距离之和为5的点（并表上相应的字母）
    （3）由以上探索解答下列问题：
    ①当|x+1|+|x-2|=7时，x=
    4或-4
    4或-4
    ； 
    ②|x-3|+|x-4|+|x-5|的和的最小值=
    2
    2

    ③求|x-1|+|x-2|+|x-3|…|x-21|的最小值．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012年四川省成都铁中八年级上学期期中检测数学卷 题型：解答题

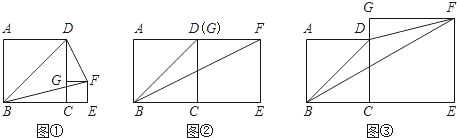
    （12分）正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上. 分别连接BD，BF，FD，得到△BFD.
    【小题1】（1）在图中，若正方形CEFG的边长分别为1，3，4，且正方形ABCD的边长均为3，请通过计算填写下表：

    正方形CEFG的边长
    		1
    		3
    		4
    △BFD的面积
    		 
    		 
    		 
    【小题2】（2）若正方形CEFG的边长为a，正方形ABCD的边长为b，猜想S△BFD的大小，并结合图证明你的猜想.

    查看答案和解析>>

    科目：初中数学 来源：2011-2012年四川省八年级上学期期中检测数学卷 题型：解答题

    （12分）正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上. 分别连接BD，BF，FD，得到△BFD.

    1.（1）在图中，若正方形CEFG的边长分别为1，3，4，且正方形ABCD的边长均为3，请通过计算填写下表：

    正方形CEFG的边长

    1

    3

    4

    △BFD的面积

     

     

     

    2.（2）若正方形CEFG的边长为a，正方形ABCD的边长为b，猜想S△BFD的大小，并结合图证明你的猜想.

     

    查看答案和解析>>

    科目：初中数学 来源：2013届四川成都铁中八年级期中检测数学卷 题型：解答题

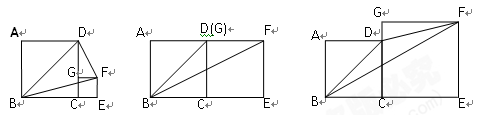
    正方形ABCD与正方形CEFG的位置如图所示，点G在线段CD或CD的延长线上. 分别连接BD，BF，FD，得到△BFD.

    1.在图1～图3中，若正方形CEFG的边长分别为1，3，4，且正方形ABCD的边长均为3，请通过计算填写下表：

    正方形CEFG的边长

    1

    3

    4

    △BFD的面积

     

     

     

    2.若正方形CEFG的边长为a，正方形ABCD的边长为b，猜想S△BFD的大小，并结合图3证明你的猜想.

     

     

    查看答案和解析>>

    同步练习册答案