
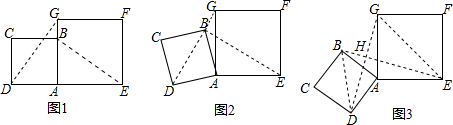
分析 (1)利用正方形得到条件,判断出△ADG≌△ABE从而∠AEB+∠ADG=90°,即可;
(2)利用正方形的性质在Rt△AMD中,∠MDA=45°,AD=2从而得出AM=$DM=\sqrt{2}$,在Rt△AMG中,AM2+GM2=AG2从而得出GM=$\sqrt{7}$即可;
(3)利用旋转,设旋转角为α,在Rt△AIB中,BI=ABsinα,在Rt△AHD中,DH=ADsinα,从而S四边形BDEG用sinα,即可.
解答 (1)如图1,延长EB交DG于点H
∵四边形ABCD与四边形AEFG是正方形
∴AD=AB,∠DAG=∠BAE=90°,AG=AE
∴△ADG≌△ABE(SAS)
∴∠AGD=∠AEB
∵△ADG中∠AGD+∠ADG=90°
∴∠AEB+∠ADG=90°
∵△DEH中,∠AEB+∠ADG+∠DHE=180°
∴∠DHE=90°
∴DG⊥BE.
(2)如图2,过点A作AM⊥DG交DG于点M,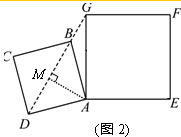
∠AMD=∠AMG=90°
∵BD是正方形ABCD的对角
∴∠MDA=45°
在Rt△AMD中,
∵∠MDA=45°,AD=2
∴AM=$DM=\sqrt{2}$
在Rt△AMG中,
∵AM2+GM2=AG2
∴GM=$\sqrt{7}$
∵DG=DM+GM=$\sqrt{2}$+$\sqrt{7}$
∴S△ADG=$\frac{1}{2}$DG•AM=$\frac{1}{2}$( $\sqrt{2}$+$\sqrt{7}$)$\sqrt{2}$=1+$\frac{1}{2}$$\sqrt{14}$
(3)如图3,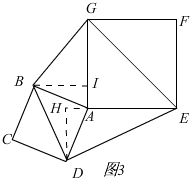
作DH⊥AE交EA的延长线与H,作BI⊥AG,
∵四边形ABCD是边长为2的正方形,
∴AB=AD=2,
设旋转角为α,
∴∠BIG=α,∠HAD=α,
在Rt△AIB中,BI=ABsinα,
在Rt△AHD中,DH=ADsinα,
∵四边形AEFG是边长为3的正方形,
∴AG=AE=3,
∴S四边形BDEG=S△ABG+S△ABD+S△ADE+S△AEG
=S△ABD+S△AEG+S△ABG+S△ADE
=$\frac{1}{2}$AB×AD+$\frac{1}{2}$AG×AE+$\frac{1}{2}$×AG×BI+$\frac{1}{2}$AE×DH
=$\frac{1}{2}$AB×AD+$\frac{1}{2}$AG×AE+$\frac{1}{2}$×AG×ABsinα+$\frac{1}{2}$AE×ADsinα
=$\frac{1}{2}$×2×2+$\frac{1}{2}$×3×3+$\frac{1}{2}$×3×2sinα+$\frac{1}{2}$×3×2sinα
=$\frac{13}{2}$+6sinα
当sinα=1时,S四边形BDEG最大,S四边形BDEG最大=$\frac{25}{2}$,
故答案为$\frac{25}{2}$.
点评 本题是四边形的综合题,主要考查正方形的性质,解本题的关键是利用三角函数表示四边形BDEG的面积,本题的难点是旋转角的利用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
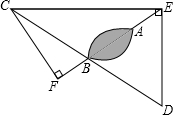 海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=$\frac{3}{5}$.
海上有一小岛,为了测量小岛两端A、B的距离,测量人员设计了一种测量方法,如图所示,已知B点是CD的中点,E是BA延长线上的一点,测得AE=10海里,DE=30海里,且DE⊥EC,cos∠D=$\frac{3}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
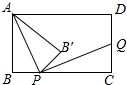 如图,在矩形ABCD中,AB=6,BC=8,点P是BC边上的一个动点(点P与点B、C都不重合),现将△PAB沿直线PA折叠,使点B落到点B′处;过点P作∠CPB′的角平分线交CD于点Q.设BP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,在矩形ABCD中,AB=6,BC=8,点P是BC边上的一个动点(点P与点B、C都不重合),现将△PAB沿直线PA折叠,使点B落到点B′处;过点P作∠CPB′的角平分线交CD于点Q.设BP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )| A. | 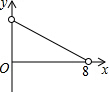 | B. | 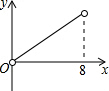 | C. | 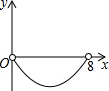 | D. | 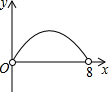 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
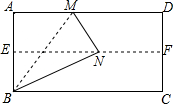 如果是我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图):
如果是我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,可以采用下面的方法(如图):查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
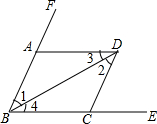 根据图填空,括号内填推理的依据.
根据图填空,括号内填推理的依据.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com