
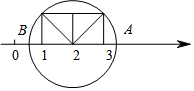
 如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画圆,与数轴相交.则圆与数轴的交点所表示的数是2+$\sqrt{2}$或2-$\sqrt{2}$.
如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画圆,与数轴相交.则圆与数轴的交点所表示的数是2+$\sqrt{2}$或2-$\sqrt{2}$. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 165根、100个 | B. | 165根、55个 | C. | 135根、85个 | D. | 145根、100个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
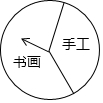 某班“红领巾义卖”活动中设立了一个可以自由转动的转盘.规定:顾客购物20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某班“红领巾义卖”活动中设立了一个可以自由转动的转盘.规定:顾客购物20元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 300 | 400 | 500 | 1000 |
| 落在“书画作品”区域的次数m | 60 | 122 | 180 | 298 | a | 604 |
| 落在“书画作品”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | b | 0.59 | 0.604 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com