
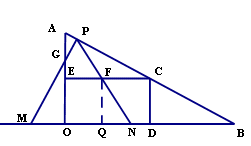
 ����ABO=30�㣮����P���߶�AB�ϴӵ�A���յ�B��ÿ��
����ABO=30�㣮����P���߶�AB�ϴӵ�A���յ�B��ÿ�� ����λ���ٶ��˶������˶�ʱ��Ϊt�룮��ֱ��OB ��ȡ����M��N���ȱߡ�PMN��
����λ���ٶ��˶������˶�ʱ��Ϊt�룮��ֱ��OB ��ȡ����M��N���ȱߡ�PMN��
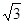 ����
����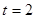 ����2�֣�
����2�֣�
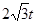 ����BP=
����BP=
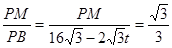
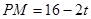 �����ȱߡ�PMN�ı߳�Ϊ
�����ȱߡ�PMN�ı߳�Ϊ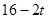 .��4�֣�
.��4�֣� ʱ����ͼAP=
ʱ����ͼAP=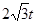 ����
����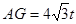
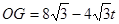 ����
����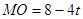 ��
��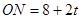 .
.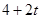 .
.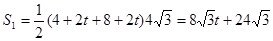
 ��0����S1��t�����������
��0����S1��t�����������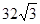 .��7�֣�
.��7�֣�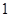 ��t��2ʱ����ͼ
��t��2ʱ����ͼ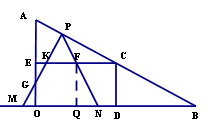
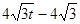 ����EK=
����EK=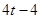 ��
��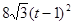 .
.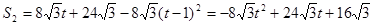 .
.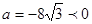 ���Գ���Ϊ
���Գ���Ϊ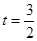 ��
��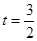 ʱ��
ʱ��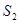 �����ֵΪ
�����ֵΪ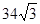 .��9�֣�
.��9�֣�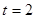 ʱ��
ʱ��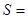
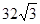 ��
��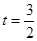 ʱ��S�����ֵΪ
ʱ��S�����ֵΪ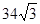 .��10�֣�
.��10�֣�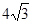 ��HN=4��
��HN=4��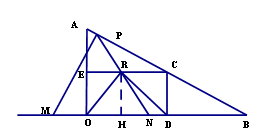
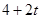 ��OD=12��DH=
��OD=12��DH=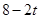 ��
��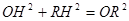 ��
��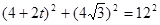 ��
��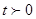 ����
����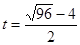 ��2������������ȥ��
��2������������ȥ��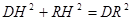 ��
��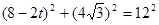 ����
����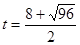 ��2����
��2����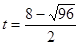 ��0��������������ȥ��
��0��������������ȥ��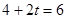 ����
����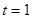 ��
��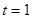 ʱ����ODR�ǵ��������Ρ���12�֣�
ʱ����ODR�ǵ��������Ρ���12�֣�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��
�� �����������κ�����ͼ���е�һ����x�ύ��A��B������ͬ�ĵ�.
�����������κ�����ͼ���е�һ����x�ύ��A��B������ͬ�ĵ�.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
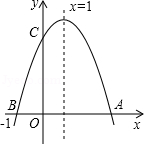
 ������B(
������B( ��2)������x�ύ�ڵ�A����������
��2)������x�ύ�ڵ�A���������� ��x��������ƽ�ƣ���ƽ�ƺ��������ΪC���䶥��ΪP��
��x��������ƽ�ƣ���ƽ�ƺ��������ΪC���䶥��ΪP��
 ƽ�ƹ����У�����PAB��ֱ��AB���۵õ���DAB����D�ܷ�����������C�ϣ����ܣ������ʱ������C����P�����ꣻ�粻�ܣ�˵�����ɣ�
ƽ�ƹ����У�����PAB��ֱ��AB���۵õ���DAB����D�ܷ�����������C�ϣ����ܣ������ʱ������C����P�����ꣻ�粻�ܣ�˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��y�ύ��C�㣬��x�ύ��A��B���㣬��A�������ǣ���1��0����O������ԭ�㣬��
��y�ύ��C�㣬��x�ύ��A��B���㣬��A�������ǣ���1��0����O������ԭ�㣬�� ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��a��0,b��0,c��0 | B�� a��0,b��0,c��0 |
| C��a��0,b��0,c��0 | D�� a��0,b��0,c��0 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 �IJ��ֶ�Ӧֵ���±���
�IJ��ֶ�Ӧֵ���±��� | �� |  | 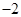 |  |  |  |  | �� |
 | �� |  |  |  |  |  |  | �� |
 ͼ��ĶԳ���Ϊ
ͼ��ĶԳ���Ϊ ��
�� ��Ӧ�ĺ���ֵ
��Ӧ�ĺ���ֵ ��
���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com