答:(1)小明和小华所取的水的初始温度分别是70℃和80℃;
在当时的条件下,水的沸点是98℃;
只有在气压低的情况下,水的沸点才不会到达100℃,∴验时实际的大气压 小于
1个标准大气压.
故答案为:小于;
(2)当0<x≤7时,y
小华=kx+80,
10k+80=98,
解得k=1.8,
∴y
小华=1.8x+80
设y
小明=kx+70,
7x+70=98,
解得:k=4,
∴y
小明=4x+70
小明实验的函数关系式为

小华实验的函数关系式为

(3)y
1>y
2,
即4x+70>1.8x+80,
得

.
即当

时,
小明做水沸腾实验的水的温度超过小华做水沸腾实验的水的温度.
(4)A、10分钟后,加热继续,温度不再上升,故错误;
B、沸腾温度不足100℃可能是气压低,故错误;
C、正确;
D、沸腾后不再成正比,故错误;
故选C.
分析:(1)看x=0时,所对应的函数值分别是多少即为所取的水的初始温度,看函数图象的最高点所对应的函数值即为水的沸点;只有在气压低的情况下,水的沸点才不会到达100°;
(2)设出2个函数关系式,分别把相应函数上的点代入即可得到相应的函数解析式;
(3)让两个函数值相等,得到交点坐标,易得在交点的右侧,小明做水沸腾实验的水的温度超过小华做水沸腾实验的水的温度;
(4)结合物理知识,找到正确选项即可.
点评:结合物理知识考查一次函数的应用;掌握不同条件下沸腾的需要的条件及原理是解决本题的关键.




 .
. 时,
时,

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案 的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象;
的图象向上平移2个单位得反比例函数______的图象,若再向右平移2个单位后可以得到反比例函数______的图象; 的图象可以由函数
的图象可以由函数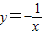 图象如何平移得到的;
图象如何平移得到的; 的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.
的图象将此函数向右平移2个单位后,再进行上下平移,使新函数的图象与坐标轴的两个交点与原点构成一个等腰三角形,求新函数的解析式.