
����Ŀ��ĸ��ǰϦ��ij�̵�ӳ��ҹ���A��B������У���֪A��B������еĵ��۱�Ϊ3��4�����ۺ�Ϊ210Ԫ��
��1����A��B������еĵ��۷ֱ��Ƕ���Ԫ��
��2�����̵깺�����������ǡ����ȥ9900Ԫ���ҹ���A��������36����B����е�����������A�����������2�������м��ֽ���������
��3�������г����飬����һ��A����пɻ���12Ԫ������һ��B����пɻ���18Ԫ��Ϊ���װ��ģ��õ�������ÿ�۳�һ��B����У�Ϊ���Ĺ��������mԪ��ÿ��A����е����䣬�ڣ�2���������£�Ҫʹ���ȫ���۳������з���������ͬ��mֵ�Ƕ��٣���ʱ������������Ԫ��
���𰸡���1��A����е���Ϊ90Ԫ��B����е���Ϊ120Ԫ;��2��������;��3��1320Ԫ��
��������
��1������A��B������еĵ��۱�Ϊ3��4�����ۺ�Ϊ210Ԫ���ó���ʽ������ɣ�
��2�������������ǡ����ȥ9900Ԫ����ϣ�1�������ó���ʽ������������е�������ϵ������ɣ�
��3�����ȱ�ʾ��������������������w��m��ϵ�ó���������Ĵ𰸣�
��1����A����е���Ϊ3xԪ��B����е���Ϊ4xԪ��
��3x+4x��210��
���x��30��
����A����е���Ϊ3��30��90Ԫ��
B����е���Ϊ4��30��120Ԫ��
��2����A������a��������B�����b����
��90a+120b��9900��
���в���ʽ��Ϊ�� ��
��
��ã�30��a��36��
��Ϊ��и���Ϊ���������Է��ϵķ�����2�֣��ֱ��ǣ�
��һ�֣�A�����30����B�����60����
�ڶ��֣�A�����34����B�����57����
��3������̵����wԪ���ɣ�2����֪��w��12a+��18��m��b��a=110-![]() ��
��
��w����2��m��b+1320��
��ʹ���з�����������ͬ������2��m��0����m��2��
��ʱ��������1320Ԫ��


 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������꼶��ʦ���Ծ���������ѧ�������������Ƚ������۵��飬��������ĿΪ�������ɡ�����˼����רע������������Ŀ��������������ȡ������������ѧ���IJ�����������Ƴ���ͼ��ʾ��Ƶ���ֲ�ֱ��ͼ������ͳ��ͼ�������������������ͼ��������Ϣ����������⣺
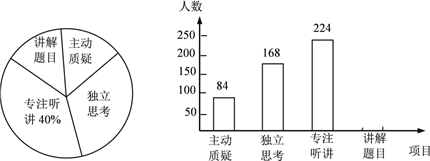
��1������������У�һ������� ��ѧ����
��2��������ͳ��ͼ�У���Ŀ���������ɡ����ڵ����ε�Բ�ĽǵĶ���Ϊ �ȣ�
��3���뽫Ƶ���ֲ�ֱ��ͼ����������
��4�����ȫ����6000������ѧ������ô���Ծ��������У�������˼�����ij���ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2��8ax+12a��a��0����x�ύ��A��B����(��A�ڵ�B�����)��������������һ��C�ڵ�һ���ޣ���ʹ��OCA�ס�OBC��
��1����OC�ij���![]() ��ֵ��
��ֵ��
��2����ֱ��BC��y�ύ��P�㣬����Cǡ����OP�Ĵ�ֱƽ������ʱ����ֱ��BP�������ߵĽ���ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ų�����ֽƬ![]() ����ͼ�٣���
����ͼ�٣���![]() ����ֽƬ�۵���ʹ
����ֽƬ�۵���ʹ![]() ����
����![]() ���ϣ�
���ϣ�![]() Ϊ
Ϊ![]() �Ķ�Ӧ�㣬�ۺ�Ϊ
�Ķ�Ӧ�㣬�ۺ�Ϊ![]() ����ͼ�ڣ����ٽ�������
����ͼ�ڣ����ٽ�������![]() ��
��![]() Ϊ�ۺ������۵�������
Ϊ�ۺ������۵�������![]() ����
����![]() �����ȷֵ��ϣ���
�����ȷֵ��ϣ���![]() �ij�Ϊ�� ��
�ij��� ��

A.8B.10C.8��10D.8��12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ij��˾�����βɹ���һ�����⣬��һ�λ���40��Ԫ���ڶ��λ���60��Ԫ����֪��һ�βɹ�ʱÿ�ִ���ļ۸��ȥ���ƽ���۸�������500Ԫ���ڶ��βɹ�ʱÿ�ִ���ļ۸��ȥ���ƽ���۸��½���500Ԫ���ڶ��βɹ��������ǵ�һ�βɹ�����������.
��1������ȥ��ÿ�ִ����ƽ���۸��Ƕ���Ԫ��
��2���ù�˾�ɽ�����ӹ�����ۻ���Ƭ���������ӹ�����ۣ�ÿ��ɼӹ�8�ִ��⣬ÿ�ִ������1000Ԫ���������ӹ�����Ƭ��ÿ��ɼӹ�12�ִ��⣬ÿ�ִ������600Ԫ.Ϊ������Ҫ�����вɹ��Ĵ��������30���ڼӹ���ϣ��Ҽӹ���۵Ĵ������������ڼӹ���Ƭ�Ĵ���������һ��.Ϊ����������Ӧ�����ٶִ���ӹ�����ۣ��������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ϣ�˼����ͬѧС���ڽ�����ȵ�ʽ���⣺����֪����![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ��ֵ��ʱ�����������������
��ֵ��ʱ�����������������![]() �������ȵ�ʽת��Ϊ��������ʽ�������õ�ʽ�Ļ����������������ֵ.�����ó�
�������ȵ�ʽת��Ϊ��������ʽ�������õ�ʽ�Ļ����������������ֵ.�����ó�![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵ���Ӷ��������.�������£�
֮��Ĺ�ϵ���Ӷ��������.�������£�
�⣻��![]() �����У�
������
![]() ��
��![]() ��
��![]() ��
��
������������ʽ��ӣ���![]() .
.
![]()
![]() ��
��![]() ��
��![]() ��������
��������
![]()
![]() ����
����![]() ��.
��.
![]()
![]() .
.
��ϸ�Ķ��������ϣ������������⣺
��1��������![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
��2����֪![]() ��
��![]() ��
��![]() ��
��![]() ������ȣ���֤��
������ȣ���֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У���ABC���������㶼�ڸ���ϣ���A��B��C������ֱ�ΪA(-2��4)��B(-2��0)��C(-4��1)�����������ƽ��ֱ������ϵ����������⣺
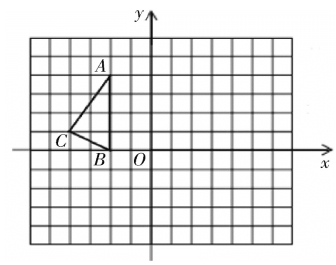
��1��������ABC����ԭ��O���ĶԳ�ͼ����A1B1C1.
��2��ƽ����ABC��ʹ��A�ƶ�����A2(0��2)������ƽ�ƺ����A2B2C2��д����B2��C2������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=1��M��N�ֱ���AD��BC�ߵ��е㣬��BQ����BCQ�۵�������Cǡ������MN�ϵĵ�P������PQ�ij�Ϊ��������
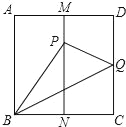
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����¶��壩��A��B��C Ϊ���������㣬���� C �� A �ľ����ǵ� C �� B �ľ���� 3 �������ǾͳƵ�
C �ǣ�A��B�������˵㣮
��������֪����
��1����ͼ 1���� A ��ʾ����Ϊ��1���� B ��ʾ����Ϊ 3����ʾ 2 �ĵ� C ���� A �ľ����� 3�� ���� B �ľ����� 1����ô�� C �ǣ�A��B�������˵㣮
�٣�B��A�������˵��ʾ������ ��A����1�� B.0�� C.1�� D.2
����˵�� A �ǣ�C��E�������˵㣮
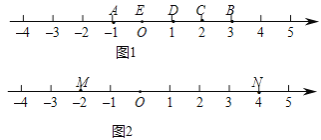
��2����ͼ 2��M��N Ϊ���������㣬�� M ����ʾ����Ϊ��2���� N ����ʾ����Ϊ 4����M��N�����ҵ�ʾ����Ϊ ��
����չӦ�ã���
��3����ͼ 3��A��B Ϊ���������㣬�� A ����ʾ����Ϊ��20���� B ����ʾ����Ϊ 40������һֻ�������� P �ӵ� B �������� 3 ����λÿ����ٶ������˶�������� A ֹͣ���� t Ϊ��ֵʱ��P��A �� B ��������ǡ����һ����Ϊ������������˵㣿

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com