
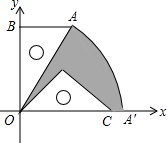
 如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π)
如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π) 分析 求出∠AOA′,根据扇形的面积公式求出扇形AOA′的面积,求出OC、DC长,求出△ODC的面积,根据:阴影部分的面积即为扇形OAA′的面积减去三角形OCD的面积计算可得.
解答 解:如图,记45°角的三角板直角顶点为D,
在Rt△OBA中,∠AOB=30°,AB=3,
∴OA=$\frac{AB}{sin∠AOB}$=$\frac{3}{\frac{1}{2}}$=6,
∴OB=OA•cos∠AOB=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$.
由题意得:∠AOC=60°,
S扇形AOA′=$\frac{60•π•{6}^{2}}{360}$=6π.
在Rt△OCD中,∠DOC=45°,OC=OB=3$\sqrt{3}$,
∴OD=OC•cos45°=3$\sqrt{3}$×$\frac{\sqrt{2}}{2}$=$\frac{3\sqrt{6}}{2}$.
∴S△ODC=$\frac{1}{2}$OD2=$\frac{1}{2}$×$(\frac{3\sqrt{6}}{2})^{2}$=$\frac{27}{4}$.
∴S阴影=S扇形AOA′-S△ODC=6π-$\frac{27}{4}$,
故答案为:6π-$\frac{27}{4}$.
点评 本题主要考查扇形面积的计算、解直角三角形的能力,在求阴影部分的面积时,常常是几个规则图形面积的和或差.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.
如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在0C上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达0C′的位置.已知0A=8cm,AB⊥0C,∠B0A=60°,sin∠B′A0=$\frac{9}{10}$,则点B′到0A的距离为( )
如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在0C上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达0C′的位置.已知0A=8cm,AB⊥0C,∠B0A=60°,sin∠B′A0=$\frac{9}{10}$,则点B′到0A的距离为( )| A. | $\frac{9\sqrt{3}}{10}$cm | B. | $\frac{18\sqrt{3}}{10}$cm | C. | $\frac{9\sqrt{3}}{5}$cm | D. | $\frac{18\sqrt{3}}{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
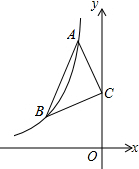 如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.
如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
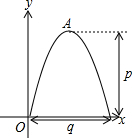 如图,一抛物线桥拱的最高点A到水面的距离为p,在水面上截得的距离为q,如图所示,建立平面直角坐标系.
如图,一抛物线桥拱的最高点A到水面的距离为p,在水面上截得的距离为q,如图所示,建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 课外阅读是提高学生素养的重要途径,某校团委为了解学生课外阅读情况,随机抽查了本校n名学生,统计它们平均每天课外阅读时间t(时),并根据时间t的长短分为A、B、C、D四类,(A)0<t<0.5,(B)0.5≤t<1,(C)1≤t<1.5,(D)t≥1.5,并根据抽查的人数绘制如下统计图.
课外阅读是提高学生素养的重要途径,某校团委为了解学生课外阅读情况,随机抽查了本校n名学生,统计它们平均每天课外阅读时间t(时),并根据时间t的长短分为A、B、C、D四类,(A)0<t<0.5,(B)0.5≤t<1,(C)1≤t<1.5,(D)t≥1.5,并根据抽查的人数绘制如下统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
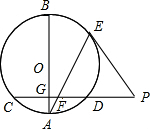 如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.
如图,AB是圆O的一条直径,弦CD垂直于AB,垂足为点G、E是劣弧BD上一点,点E处的切线与CD的延长线交于点P,连接AE,交CD于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com