
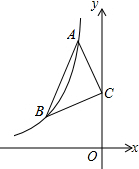
 如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.
如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$. 分析 过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,根据角的计算得出“∠ACD=∠CBE,∠BCE=∠CAD”,由此证出△ACD≌△CBE;再设点B的坐标为(m,-$\frac{6}{m}$),由三角形全等找出点A的坐标,将点A的坐标代入到反比例函数解析式中求出m的值,将m的值代入B点坐标即可得出点B的坐标,结合等腰直角三角形的性质以及两点间的距离公式即可得出结论.
解答 解:过点A作AD⊥y轴于点D,过点B作BE⊥y轴于点E,如图所示.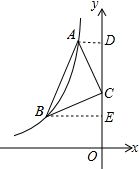
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥y轴,BE⊥y轴,
∴∠ACD+∠CAD=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,∠BCE=∠CAD.
在△ACD和△CBE中,由$\left\{\begin{array}{l}{∠CAD=∠BCE}\\{AC=CB}\\{∠ACD=∠CBE}\end{array}\right.$,
∴△ACD≌△CBE(ASA).
设点B的坐标为(m,-$\frac{6}{m}$)(m<0),则E(0,-$\frac{6}{m}$),点D(0,3-m),点A(-$\frac{6}{m}$-3,3-m),
∵点A(-$\frac{6}{m}$-3,3-m)在反比例函数y=-$\frac{6}{x}$上,
∴3-m=-$\frac{6}{-\frac{6}{m}-3}$,解得:m=-3,m=2(舍去).
∴点B的坐标为(-3,2),
∴AB=$\sqrt{2}$BC=$\sqrt{2}$$\sqrt{(-3-0)^{2}+(2-3)^{2}}$=2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 本题考查了反比例函数的性质、全等三角形的判定及性质、等腰直角三角形的性质以及两点间的距离公式,解题的关键是求出点B的坐标.本题属于基础题,难度不大,解决该题型题目时,设出反比例函数图象上一点的坐标,根据边角关系表示出来另一点的坐标,再结合点在反比例函数图象上得出点的坐标,最后由两点间的距离公式求出线段的长度即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
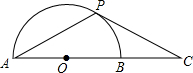 如图,已知⊙O中,P是半圆AB上一动点,C是AB延长线上一点,PC=PA
如图,已知⊙O中,P是半圆AB上一动点,C是AB延长线上一点,PC=PA查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
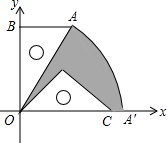 如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π)
如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3,若把含30°的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好与x轴重叠,点A落在点A′处,则图中阴影部分的面积为6π-$\frac{27}{4}$(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A(2,n)在反比例函数y=$\frac{3}{x}$的图象上,点B在第二象限,∠AOB=90°,∠OBA=30°,在小组合作学习中,四位同学发现并提出了以下四个结论,其中正确的有( )个.
如图,点A(2,n)在反比例函数y=$\frac{3}{x}$的图象上,点B在第二象限,∠AOB=90°,∠OBA=30°,在小组合作学习中,四位同学发现并提出了以下四个结论,其中正确的有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com