
����Ŀ����ͼ��������OABC��OA����x����������ϣ�OC��y����������ϣ�������y=ax2+bx������B��1��4���͵�E��3��0�����㣮
��1���������ߵĽ���ʽ��
��2������D���߶�OC�ϣ���BD��DE��BD=DE����D������ꣻ
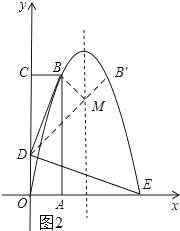
��3����������2���£��������ߵĶԳ�������һ��M��ʹ�á�BDM���ܳ�Ϊ��С�������BDM�ܳ�����Сֵ����ʱ��M�����ꣻ
��4����������2���£���B�㵽E����������ߵ�ͼ���ϣ��Ƿ����һ����P��ʹ�á�PAD�������������ڣ��������PAD��������ֵ����ʱP������ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺����B��1��4����E��3��0����������������ߵĽ���ʽ�ã� ![]() ��
��
��ã� ![]() ��
��
�����ߵĽ���ʽΪy=��2x2+6x
��2��
�⣺��ͼ1��ʾ��

��BD��DE��
���BDE=90�㣮
���BDC+��EDO=90�㣮
�֡ߡ�ODE+��DEO=90�㣬
���BDC=��DE0��
�ڡ�BDC�͡�DOE�У�  ��
��
���BDC�ա�DEO��
��OD=AO=1��
��D��0��1����
��3��
�⣺��ͼ2��ʾ������B���������ߵĶԳ���ĶԳƵ�B�䣬����B��D�������ߵĶԳ������M��
��x=�� ![]() =
= ![]() ��
��
���B���������2��4����
�ߵ�B���B�����x= ![]() �Գƣ�
�Գƣ�
��MB=B��M��
��DM+MB=DM+MB�䣮
�൱��D��M��B����һ��ֱ����ʱ��MD+MB����Сֵ������BMD���ܳ�����Сֵ����
���������ľ��빫ʽ��֪��BD= ![]() =
= ![]() ��DB��=
��DB��= ![]() =
= ![]() ��
��
���BDM����Сֵ= ![]() +
+ ![]() ��
��
��ֱ��B��D�Ľ���ʽΪy=kx+b��
����D��B����������ã� ![]() ��
��
��ã�k= ![]() ��b=1��
��b=1��
��ֱ��DB��Ľ���ʽΪy= ![]() x+1��
x+1��
��x= ![]() ����ã�y=
����ã�y= ![]() ��
��
��M�� ![]() ��
�� ![]() ��
��
��4��
��ͼ3��ʾ������F��FG��x�ᣬ����ΪG��
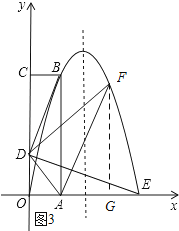
���F��a����2a2+6a������OG=a��FG=��2a2+6a��
��S����DOGF= ![]() ��OD+FG��OG=
��OD+FG��OG= ![]() ����2a2+6a+1����a=��a3+3a2+
����2a2+6a+1����a=��a3+3a2+ ![]() a��S��ODA=
a��S��ODA= ![]() ODOA=
ODOA= ![]() ��1��1=
��1��1= ![]() ��S��AGF=
��S��AGF= ![]() AGFG=��a3+4a2��3a��
AGFG=��a3+4a2��3a��
��S��FDA=S����DOGF��S��ODA��S��AGF=��a2+ ![]() a��
a�� ![]() ��
��
�൱a= ![]() ʱ��S��FDA�����ֵΪ
ʱ��S��FDA�����ֵΪ ![]() ��
��
���P�������� ![]() ��
�� ![]() ����
����
����������1������B��1��4����E��3��0����������������ߵĽ���ʽ���õ�����a��b�ķ����飬���a��b��ֵ���Ӷ��ɵõ������ߵĽ���ʽ����2������ͬ�ǵ�������֤����BDC=��DE0��Ȼ��������AAS֤����BDC�ա�DEO���Ӷ��õ�OD=AO=1�����ǿ���õ�D�����ꣻ��3������B���������ߵĶԳ���ĶԳƵ�B�䣬����B��D�������ߵĶԳ������M������������ߵĶԳ��᷽�̣��Ӷ��õ���B������꣬����ԳƵ����ʿ�֪����D��M��B����һ��ֱ����ʱ����BMD���ܳ�����Сֵ�����������ľ��빫ʽ���BD��B��D�ij��ȣ��Ӷ��õ������ε��ܳ���Сֵ��Ȼ�����ݴ���ϵ�������D��B��Ľ���ʽ��Ȼ��M�ĺ�����������õ�M�������ꣻ��4������F��FG��x�ᣬ����ΪG�����F��a����2a2+6a������OG=a��FG=��2a2+6a��Ȼ������S��FDA=S����DOGF��S��ODA��S��AGF�������ε������a�ĺ�����ϵʽ��Ȼ�����ݶ��κ�����������⼴�ɣ�������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ��������κ�����һ�κ����Ľ���ʽ��ȫ�������ε����ʺ��ж�����ԳƵ����ʡ����κ�����ͼ������ʵõ���FDA�������a�ĺ�����ϵʽ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У�OA=3��OC=2��F��AB�ϵ�һ�����㣨F����A��B�غϣ�������F�ķ���������y= ![]() ��k��0����ͼ����BC�߽��ڵ�E��
��k��0����ͼ����BC�߽��ڵ�E��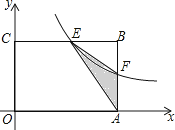
��1����FΪAB���е�ʱ����ú����Ľ���ʽ��
��2����kΪ��ֵʱ����EFA���������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�E��AD��һ�㣬�ӳ�CE����F��ʹ��FBC=��DCE��
��1����֤����D=��F��
��2����ֱ�ߺ�Բ����AD������һ��P��ʹ��BPC�ס�CDP��������ͼ�ĺۼ�����д��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ʽ�� 
��1����ʽ��Ľ⼯����д���������������⣻
��2���ڲ���ʽ�����������������ȡ������ͬ��������ˣ����û���״ͼ���б��ķ������Ϊ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O���߶�AB���߶�CD���е㣮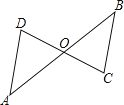
��1����֤����AOD�ա�BOC��
��2����֤��AD��BC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽������ȫ�д�������������̶ȣ�ij��ѧ��ѧ��ȤС����ȫ�мס����������ڽ����˵���ͳ�ƣ�����������Ϊ�����⣬һ�㣬���⣬�dz��������࣬���ա�������ȫ���ʾ��õ����в�������ͳ��ͼ��
����ͼ����Ϣ������������⣺
��1����˴ε����н��ܵ����������
��2����˴ε����н��Ϊ�dz������������
��3����ȤС�����ӵ�����Ϊ�������4λ���������ѡ��2Ϊ���лطã���֪4Ϊ��������2λ���Լ�������2λ���������������б����û���״ͼ�ķ������ѡ�����������Լ����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�κ��Ͼ���ѧϰ�ڼ䣬�Ҿ�Ϊȷ����OBC�����ڵİ�ȫ������Dz���Ҿ����ֱ���O��B��C����ء�OBC�������״���ʾͼ�ϣ�����B�ھ���O����������80���ﴦ������C�ھ���B����������60���ﴦ�����Ҿ�����װ������ͬ��̽���״�״����Ч̽�ⷶΧ�ǰ뾶Ϊr��Բ������ֻ�����ں�ƽ���ϵ�̽�⣩
��1�������Ҿ���Ҫ�ԡ�OBC���������ä���أ����״����Ч̽��뾶r����Ϊ���ٺ��
��2������һ�ҵн�A�Ӷ����ӽ���OBC������ijһʱ�̾���B���Aλ�ڱ�ƫ��60�㷽���ϣ�ͬʱ����C���Aλ����ƫ��30�㷽���ϣ����ʱ�н�A���OBC�������̾���Ϊ���ٺ��
��3�����н�A����̾����·����20 ![]() ����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15��ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
����/Сʱ���ٶȿ�����OBC�����Ҿ�����B�ر�ƫ��15��ķ����н����أ���B�����ٶ�����Ϊ���ٲ����ڴ˷��������ص��н�A��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ ![]() ��ͼ����ͼ��ʾ�����ڸú��������н�����ȷ����������ţ��� �ٺ���ͼ������Գ�ͼ�Σ��ں���ͼ�������ĶԳ�ͼ�Σ��۵�x��0ʱ����������Сֵ���ܵ㣨1��4���ں���ͼ���ϣ��ݵ�x��1��x��3ʱ��y��4��
��ͼ����ͼ��ʾ�����ڸú��������н�����ȷ����������ţ��� �ٺ���ͼ������Գ�ͼ�Σ��ں���ͼ�������ĶԳ�ͼ�Σ��۵�x��0ʱ����������Сֵ���ܵ㣨1��4���ں���ͼ���ϣ��ݵ�x��1��x��3ʱ��y��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��12������ ![]() ��+8��2��2������1��2
��+8��2��2������1��2
��2���ⲻ��ʽ ![]() ��
�� ![]() ������������������⣮
������������������⣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com