
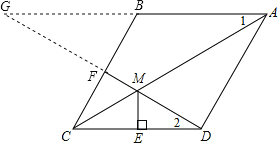
【题目】已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.

【答案】(1)解:∵四边形ABCD是菱形,
∴AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠ACD=∠2,
∴MC=MD,
∵ME⊥CD,
∴CD=2CE,
∵CE=1,
∴CD=2,
∴BC=CD=2;
(2)证明:如图,∵F为边BC的中点,
∴BF=CF=![]() BC,
BC,
∴CF=CE,
在菱形ABCD中,AC平分∠BCD,
∴∠ACB=∠ACD,
在△CEM和△CFM中,
∵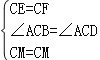 ,
,
∴△CEM≌△CFM(SAS),
∴ME=MF,
延长AB交DF于点G,
∵AB∥CD,
∴∠G=∠2,
∵∠1=∠2,
∴∠1=∠G,
∴AM=MG,
在△CDF和△BGF中,
∵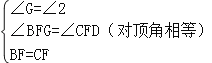 ,
,
∴△CDF≌△BGF(AAS),
∴GF=DF,
由图形可知,GM=GF+MF,
∴AM=DF+ME.
【解析】(1)根据菱形的对边平行可得AB∥D,再根据两直线平行,内错角相等可得∠1=∠ACD,所以∠ACD=∠2,根据等角对等边的性质可得CM=DM,再根据等腰三角形三线合一的性质可得CE=DE,然后求出CD的长度,即为菱形的边长BC的长度;
(2)先利用“边角边”证明△CEM和△CFM全等,根据全等三角形对应边相等可得ME=MF,延长AB交DF于点G,然后证明∠1=∠G,根据等角对等边的性质可得AM=GM,再利用“角角边”证明△CDF和△BGF全等,根据全等三角形对应边相等可得GF=DF,最后结合图形GM=GF+MF即可得证.


科目:初中数学 来源: 题型:
【题目】2015年6月国家主席习大大和比利时国王菲利普,在人民大会堂共同见证了两国公司在集成电路方面进行合作研发的签约仪式,两国将共同着力研发14纳米量产技术,这标志着我国芯片制造能力将进入国际顶尖水平.14纳米为0.000 000 014米,将0.000 000 014用科学记数法表示应为( )
A.0.14×10﹣7
B.1.4×10﹣8
C.0.014×10﹣6
D.14×10﹣9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算中,正确的是( )
A. a2+a2=2a4
B. (a-b)2=a2-b2
C. (-x6)(-x)2=x8
D. (-2a2b)3÷4a5=-2ab3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com