
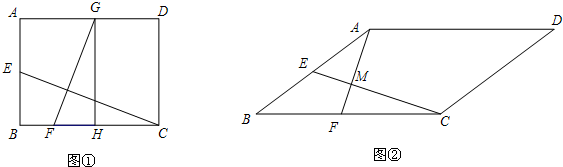
分析 (1)由余角的性质可得∠BEC=∠GFH,根据AA可证△BEC∽△HFG,根据相似三角形的性质即可求得FH的长;
(2)作AT⊥BC,ER⊥BC,由余角的性质可得∠BEC=∠GFH,根据AA可证△BEC∽△HFG,根据相似三角形的性质即可求得FT的长,再根据线段的和差关系可得BF的长.
解答 解:(1)如图①,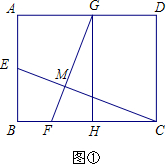
∵∠FMC=∠B=90°,
∵∠GFH+∠BCE=∠BEC+∠BCE=90°,
∴∠BEC=∠GFH,
∴△BEC∽△HFG,
∴$\frac{BE}{FH}$=$\frac{BC}{GH}$,即$\frac{2.5}{FH}$=$\frac{6.5}{5}$,
解得FH=$\frac{25}{13}$;
(2)作AT⊥BC,ER⊥BC.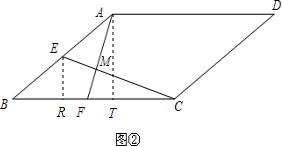
∵∠ERC=∠ATF=90°,
∵∠REC+∠RCE=∠AFC+∠FCE=90°,
∴∠REC=∠AFC,
∴△REC∽△TFA,
∴$\frac{RE}{FT}$=$\frac{RC}{AT}$,
∵AT=ABsinB=3,BT=4,ER=1.5,CR=4.5,
∴$\frac{1.5}{FT}$=$\frac{4.5}{3}$,
解得FT=1,
BF=BT-FT=3.
点评 考查了相似三角形的判定与性质,本题关键是要懂得找相似三角形,利用相似三角形的性质求解.


科目:初中数学 来源: 题型:选择题
| A. |  | B. | 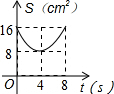 | C. | 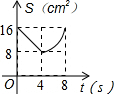 | D. | 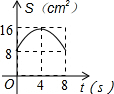 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
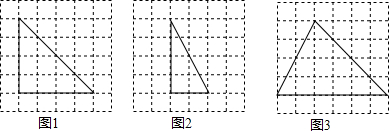
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当你打开电视机,正在播放连续剧 | |
| B. | 太阳从东边出来 | |
| C. | 绵阳出现极昼天气 | |
| D. | 随意翻开一本书的某页,这页的页码是偶数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com