
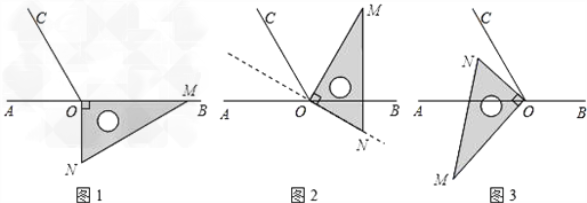
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_________(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:
∠AOM与∠NOC之间的数量关系,并说明理由。
【答案】(1) ON平分∠AOC.理由见解析;(2)40或10,(3)∠AOM -∠NOC=30°.理由见解析.
【解析】试题分析:(1)由角的平分线的定义和等角的余角相等求解;
(2)由∠BOC=120°可得∠AOC=60°,则∠RON=30°,即旋转60°或240°时ON平分∠AOC,据此求解;
(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°-∠AON、∠NOC=60°-∠AON,然后作差即可.
试题解析:(1)直线ON平分∠AOC.理由:
设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵OM⊥ON,
∴∠MOD=∠MON=90°,
∴∠COD=∠BON,
又∵∠AOD=∠BON(对顶角相等),
∴∠COD=∠AOD,
∴OD平分∠AOC,
即直线ON平分∠AOC.
(2)∵∠BOC=120°
∴∠AOC=60°,
∴∠BON=∠COD=30°,
即旋转60°时ON平分∠AOC,
由题意得,6t=60°或240°,
∴t=10或40;
(3)∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°-∠AON、∠NOC=60°-∠AON,
∴∠AOM-∠NOC=(90°-∠AON)-(60°-∠AON)=30°.


科目:初中数学 来源: 题型:
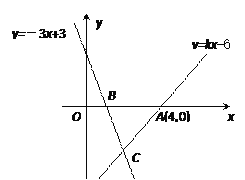
【题目】如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(1)求k的值.
(2)求△ABC的面积.
(3)在直线y=kx-6上是否存在异于点C的另一点P,使得△ABP与△ABC的面积相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场国庆节搞促销活动,购物不超过200元不给优惠,超过200(不含200元)元而不足500元,所有商品按购物价优惠10%,超过500元的,其中500元按9折优惠,超过的部分按8折优惠,A,B两个商品价格分别为180元,550元。
(1) 某人第一次购买一件A商品,第二次购买一件B商品,实际共付款多少元?
(2) 若此人一次购物购买A,B商品各一件,则实际付款多少钱?
(3) 国庆期间,某人在该商场两次购物分别付款180元和550元,如果他合起来一次性购买同样的商品,还可节约多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用 6000 元购进一批衬衫,以 60 元/件的价格出售,很快售完,然后又用 13500元购进同款衬衫,购进数量是第一次的 2 倍,购进的单价比上一次每件多 5 元,服装店 仍按原售价 60 元/件出售,并且全部售完.
(1)该服装店第一次购进衬衫多少件?
(2)将该服装店两次购进衬衫看作一笔生意,那么这笔生意是盈利还是亏损?求出盈利(或 亏损)多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=kx2﹣6x+3,若k在数组(﹣3,﹣2,﹣1,1,2,3,4)中随机取一个,则所得抛物线的对称轴在直线x=1的右方时的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,∠A=30°,点D是AB边的中点.
(1)如图1,若CD=4,求△ACB的周长.
(2)如图2,若E为AC的中点,将线段CE以C为旋转中心顺时针旋转60°,使点E至点F处,连接BF交CD于点M,连接DF,取DF的中点N,连接MN,求证:MN=2CM.
(3)如图3,以C为旋转中心将线段CD顺时针旋转90°,使点D至点E处,连接BE交CD于M,连接DE,取DE的中点N,连接交MN,试猜想BD、MN、MC之间的关系,直接写出其关系式,不证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com