
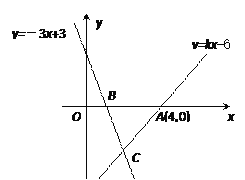
【题目】如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(1)求k的值.
(2)求△ABC的面积.
(3)在直线y=kx-6上是否存在异于点C的另一点P,使得△ABP与△ABC的面积相等,请直接写出点P的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,P点坐标(6,3).
;(3)存在,P点坐标(6,3).
【解析】(1)直接把A点坐标代入y=kx﹣6即可求出k;
(2)先确定B点坐标,再解方程组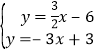 确定C的坐标为(2,﹣3),然后根据三角形面积公式计算;
确定C的坐标为(2,﹣3),然后根据三角形面积公式计算;
(3)设P点坐标为(a,b),利用△ABP与△ABC的面积相等得到![]() ×3×|b|=
×3×|b|=![]() ,解得b=3或b=﹣3(舍去),然后把y=3代入y=
,解得b=3或b=﹣3(舍去),然后把y=3代入y=![]() x﹣6即可得到P点的横坐标.
x﹣6即可得到P点的横坐标.
(1)把A(4,0)代入y=kx﹣6得:0=4k﹣6,解得:k=![]() ;
;
(2)把y=0代入y=﹣3x+3得:﹣3x+3=0,解得:x=1,∴B点坐标为(1,0),解方程组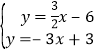 得
得![]() ,∴C的坐标为(2,﹣3),∴△ABC的面积=
,∴C的坐标为(2,﹣3),∴△ABC的面积=![]() ×3×(4﹣1)=
×3×(4﹣1)=![]() ;
;
(3)存在.
设P点坐标为(a,b).
∵△ABP与△ABC的面积相等,∴![]() ×3×|b|=
×3×|b|=![]() ,∴b=3或b=﹣3(舍去),把y=3代入y=
,∴b=3或b=﹣3(舍去),把y=3代入y=![]() x﹣6得:
x﹣6得:![]() x﹣6=3,解得:x=6,∴P点坐标(6,3).
x﹣6=3,解得:x=6,∴P点坐标(6,3).


科目:初中数学 来源: 题型:
【题目】某银行去年新增加居民存款10亿元人民币.
(1)经测量,100张面值为100元的新版人民币大约厚0.9厘米,如果将10亿元面值为100元的新版人民币摞起来,大约有多高?
(2)一台激光点钞机的点钞速度是8×104张/时,按每天点钞5小时计算,如果让点钞机点一遍10亿元面值为100元的新版人民币,点钞机大约要点多少天?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,E、F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC等于( )
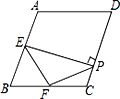
A. 45° B. 35° C. 55° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组建了书法、音乐、美术、舞蹈、演讲五个社团,全校每一名学生都参加且只参加了其中一个社团的活动.校团委从全校学生中随机选取部分学生进行了参加活动情况的调查,并将调查结果制成了如图不完整的统计图.请根据统计图完成下列问题:
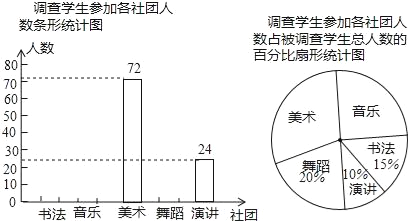
(1)参加本次调查有 名学生?
(2)根据调查数据分析,被调查的学生中有 名学生参加了音乐社团?
(3)请你补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在△ABC中,AC=3、AB=4、BC=5, P为BC上一动点,PG⊥AC于点G,PH⊥AB
于点H,M是GH的中点,P在运动过程中PM的最小值为( )
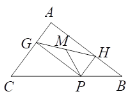
A. 2.4 B. 1.4
C. 1.3 D. 1.2
【答案】D
【解析】分析: 由AC=3、AB=4、BC=5,得AC2+AB2=BC2,则∠A=90°,再结合PG⊥AC,PH⊥AB,可证四边形AGPH是矩形;连接AP,可知当AP⊥BC时AP最短,结合矩形的两对角线相等和面积法,求出GH的值,
详解:∵AC=3、AB=4、BC=5,
∴AC2=9,AB2=16,BC2=25,
∴AC2+AB2=BC2,
∴∠A=90°.
∵PG⊥AC,PH⊥AB,
∴∠AGP=∠AHP=90° ,
∴四边形AGPH是矩形.
连接AP,
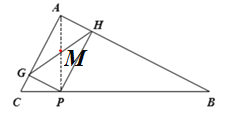
∴GH=AP.
∵当AP⊥BC时,AP最短,
∴3×4=5AP,
∴AP=![]() ,
,
∴PM的最小值为1.2.
故选D.
点睛: 本题考查了勾股定理的逆定理,矩形的判定与性质,垂线段最短,面积法求线段的长,需结合矩形的判定方法,矩形的性质以及三角形面积的知识求解;确定出点P的位置是解答本题的关键.
【题型】单选题
【结束】
18
【题目】计算:
(1)![]() (2)
(2)![]()
(3)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)求值:2 ![]() sin45°+(﹣3)2﹣20170×|﹣4|+
sin45°+(﹣3)2﹣20170×|﹣4|+ ![]() ;
;
(2)先化简,再求值:( ![]() ﹣x﹣1)÷
﹣x﹣1)÷ ![]() ,其中x是不等式组
,其中x是不等式组 ![]() 的一个整数解.
的一个整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1、2、3,…是由花盆摆成的图案,图1中有1盆花,图2中有7盆花,图3中有19盆花,……
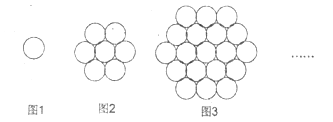
根据图中花盆摆放的规律,图4中,应该有__________盆花;第n个图形中应该有_________盆花。
查看答案和解析>>
科目:初中数学 来源: 题型:
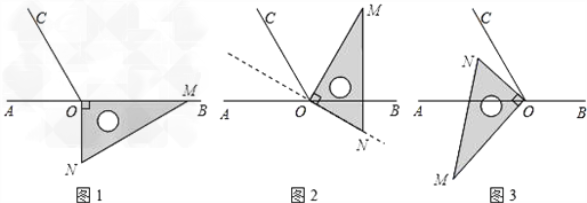
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.
(2)将图1中的三角板绕点O以每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_________(直接写出结果).
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:
∠AOM与∠NOC之间的数量关系,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com