
【题目】如图,在菱形ABCD中,∠A=110°,E、F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC等于( )
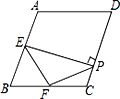
A. 45° B. 35° C. 55° D. 50°
【答案】C
【解析】延长PF交AB的延长线于点G.根据已知可得∠B,∠BEF,∠BFE的度数,再根据余角的性质可得到∠EPF的度数,从而不难求得∠FPC的度数.
延长PF交AB的延长线于点G.
在△BGF与△CPF中,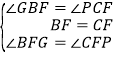 ,∴△BGF≌△CPF(ASA),∴GF=PF,∴F为PG中点.
,∴△BGF≌△CPF(ASA),∴GF=PF,∴F为PG中点.
又∵由题可知,∠BEP=90°,∴EF=![]() PG(直角三角形斜边上的中线等于斜边的一半).
PG(直角三角形斜边上的中线等于斜边的一半).
∵PF=![]() PG(中点定义),∴EF=PF,∴∠FEP=∠EPF.
PG(中点定义),∴EF=PF,∴∠FEP=∠EPF.
∵∠BEP=∠EPC=90°,∴∠BEP﹣∠FEP=∠EPC﹣∠EPF,即∠BEF=∠FPC.
∵四边形ABCD为菱形,∴AB=BC,∠ABC=180°﹣∠A=70°.
∵E,F分别为AB,BC的中点,∴BE=BF,∠BEF=∠BFE=![]() (180°﹣70°)=55°,∴∠FPC=55°.
(180°﹣70°)=55°,∴∠FPC=55°.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图![]() ,点
,点![]() 是线段
是线段![]() 上一定点,
上一定点,![]() ,
,![]() 、
、![]() 两点分别从
两点分别从![]() 、
、![]() 出发以
出发以![]() 、
、![]() 的速度沿直线
的速度沿直线![]() 向左运动,运动方向如箭头所示(
向左运动,运动方向如箭头所示(![]() 在线段
在线段![]() 上,
上,![]() 在线段
在线段![]() 上)
上)
![]() 若
若![]() ,当点
,当点![]() 、
、![]() 运动了
运动了![]() ,此时
,此时![]() ________,
________,![]() ________;(直接填空)
________;(直接填空)
![]() 当点
当点![]() 、
、![]() 运动了
运动了![]() ,求
,求![]() 的值.
的值.
![]() 若点
若点![]() 、
、![]() 运动时,总有
运动时,总有![]() ,则
,则![]() ________(填空)
________(填空)
![]() 在
在![]() 的条件下,
的条件下,![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的保护美丽图画的邛海湿地,西昌市污水处理厂决定先购买A、B两型污水处理设备共20台,对邛海湿地周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.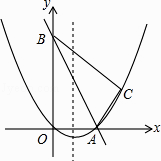
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
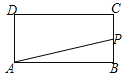
【题目】如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B![]() C
C![]() D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积![]() 与点P运动的路程之间的函数图象大致是( ).
与点P运动的路程之间的函数图象大致是( ).
A. 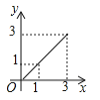 B.
B. 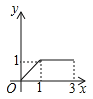 C.
C. 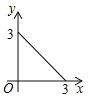 D.
D. 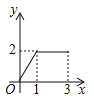
查看答案和解析>>
科目:初中数学 来源: 题型:
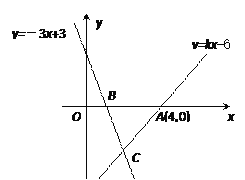
【题目】如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(1)求k的值.
(2)求△ABC的面积.
(3)在直线y=kx-6上是否存在异于点C的另一点P,使得△ABP与△ABC的面积相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB的中点,点D在线段CB上.
![]()
(1)图中共有 条线段.
(2)图中AD=AC+CD,BC=AB﹣AC,类似地,请你再写出两个有关线段的和与差的关系式:
① ;② .
(3)若AB=8,DB=1.5,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场国庆节搞促销活动,购物不超过200元不给优惠,超过200(不含200元)元而不足500元,所有商品按购物价优惠10%,超过500元的,其中500元按9折优惠,超过的部分按8折优惠,A,B两个商品价格分别为180元,550元。
(1) 某人第一次购买一件A商品,第二次购买一件B商品,实际共付款多少元?
(2) 若此人一次购物购买A,B商品各一件,则实际付款多少钱?
(3) 国庆期间,某人在该商场两次购物分别付款180元和550元,如果他合起来一次性购买同样的商品,还可节约多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com