
����Ŀ��Ϊ�˸��õı�������ͼ��������ʪ�أ���������ˮ�����������ȹ���A��B������ˮ�����豸��20̨��������ʪ���ܱ���ˮ���д�����ÿ̨A����ˮ�����豸12��Ԫ��ÿ̨B����ˮ�����豸10��Ԫ����֪1̨A����ˮ�����豸��2̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ640�֣�2̨A����ˮ�����豸��3̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ1080�֣�
��1����A��B������ˮ�����豸ÿ�ֱܷ���Դ�����ˮ���ٶ֣�
��2����Ԥ�㣬����ˮ�����������豸���ʽ���230��Ԫ��ÿ�ܴ�����ˮ����������4500�֣������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ��٣�
���𰸡�
��1���⣺��A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮx�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮy�֣�
![]() ��ã�
��ã� ![]()
��A����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ240�֣�B����ˮ�����豸ÿ��ÿ̨���Դ�����ˮ200�֣�
��2���⣺�蹺��A����ˮ�����豸x̨������B����ˮ�����豸��20��x��̨��
�� ![]()
��ã�12.5��x��15��
��һ�ַ�������x=13ʱ��20��x=7�����ѵķ���Ϊ��13��12+7��10=226��Ԫ��
�ڶ��ַ�������x=14ʱ��20��x=6�����ѵķ���Ϊ��14��12+6��10=228��Ԫ��
�����ַ�������x=15ʱ��20��x=5�����ѵķ���Ϊ��15��12+5��10=230��Ԫ��
������A����ˮ�����豸13̨������B����ˮ�����豸7̨ʱ�����蹺���ʽ����٣�������226��Ԫ
����������1������1̨A����ˮ�����豸��2̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ640�֣�2̨A����ˮ�����豸��3̨B����ˮ�����豸ÿ�ܿ��Դ�����ˮ1080�֣������г���Ӧ�Ķ�Ԫһ�η����飬�Ӷ�����⣻��2��������������г���Ӧ�IJ���ʽ�飬�Ӷ����Եõ��������Ӷ��������ÿ�ַ��������ʽ𣬴Ӷ����Խ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ��a����ͼ��b����ͼ��c����������״����С��ȫ��ͬ�ķ���ֽ������ֽ�е�ÿ��С�����εı߳���Ϊ1������ͼ��a����ͼ��b����ͼ��c���У��ֱ�����Ҫ����1������2������3����ͼ�Σ�����ͼ�θ���������뷽��ֽ�е�С�����ζ����غϣ�



��1����һ���ױ�Ϊ4�����Ϊ8�ĵ��������Σ�
��2����һ�����Ϊ10�ĵ���ֱ�������Σ�
��3����һ�����Ϊ12��ƽ���ı��Ρ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ѧ���Դ�ѧϰ��̬��һֱ�ǽ���������Ϊ��ע��һ�����⣮Ϊ���н����ֶԱ��в���ѧУ�İ��꼶ѧ���Դ�ѧϰ��̬�Ƚ�����һ�γ������飨��ѧϰ̬�ȷ�Ϊ�����㼶��A����ϲ����B������̫ϲ����C������ϲ�������������������Ƴ�ͼ1��ͼ2��ͳ��ͼ�����������������ͼ���ṩ����Ϣ������������⣺ 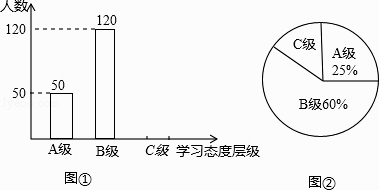
��1���˴γ��������У�����������ѧ����
��2����ͼ�ٲ���������
��3�����ͼ����C����ռ��Բ�ĽǵĶ�����
��4�����ݳ�����������������Ƹ��н�80000���������д�Լ�ж�����ѧ��ѧϰ̬�ȴ�꣨������A����B������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ȥ�������Ӿ�����10��Ԫ����ң�
(1)��������100����ֵΪ100Ԫ���°�����Ҵ�Լ��0.9���ף������10��Ԫ��ֵΪ100Ԫ���°����������������Լ�ж�ߣ�
(2)һ̨����㳮���ĵ㳮�ٶ���8��104��/ʱ����ÿ��㳮5Сʱ���㣬����õ㳮����һ��10��Ԫ��ֵΪ100Ԫ���°�����ң��㳮����ԼҪ������죿

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABD�У�AB=AD, ����ABD��BD���ۣ�ʹ��A���۵���C. E��BD��һ�㣬��BE>DE������CE���ӳ���AD��F������AE.
��1�������ⲹȫͼ�Σ�
��2���жϡ�DFC���BAE�Ĵ�С��ϵ������֤����
��3������BAD=120�㣬AB=2��ȡAD���е�G������EG����EA+EG����Сֵ.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���A=110�㣬E��F�ֱ��DZ�AB��BC���е㣬EP��CD�ڵ�P,���FPC������ ��
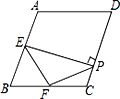
A. 45�� B. 35�� C. 55�� D. 50��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ����ABC�У�AC=3��AB=4��BC=5�� PΪBC��һ���㣬PG��AC�ڵ�G��PH��AB
�ڵ�H��M��GH���е㣬P���˶�������PM����СֵΪ�� ��
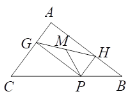
A. 2.4 B. 1.4
C. 1.3 D. 1.2
���𰸡�D
������������: ��AC=3��AB=4��BC=5����AC2+AB2=BC2������A=90�㣬�ٽ��PG��AC��PH��AB����֤�ı���AGPH�Ǿ��Σ�����AP����֪��AP��BCʱAP��̣���Ͼ��ε����Խ�����Ⱥ�����������GH��ֵ��
���:��AC=3��AB=4��BC=5��
��AC2=9��AB2=16��BC2=25��
��AC2+AB2=BC2��
���A=90��.
��PG��AC��PH��AB��
���AGP=��AHP=90�� ��
���ı���AGPH�Ǿ���.
����AP��
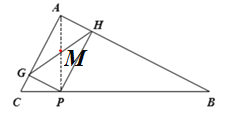
��GH=AP.
�ߵ�AP��BCʱ��AP��̣�
��3��4=5AP��
��AP=![]() ��
��
��PM����СֵΪ1.2.
��ѡD.
�㾦: ���⿼���˹��ɶ������涨�������ε��ж������ʣ����߶���̣���������߶εij������Ͼ��ε��ж����������ε������Լ������������֪ʶ��⣻ȷ������P��λ���ǽ����Ĺؼ�.
�����͡���ѡ��
��������
18
����Ŀ�����㣺
��1��![]() ��2��
��2��![]()
��3��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ͼ1����M��N���߶�AB�ָ��AM��MN��BN������AM��MN��BNΪ�ߵ���������һ��ֱ�������Σ���Ƶ�M��N���߶�AB�Ĺ��ɷָ��.
�����������⣺
��1����֪��M��N���߶�AB�Ĺ��ɷָ�㣬��BN>MN>AM.��AM=2��MN=3����BN�ij���
��2����ͼ2������F��M��N��G�ֱ���AB��AD��AE��AC���ϵ��е㣬��D��E���߶�BC�Ĺ��ɷָ�㣬��EC>DE>BD����֤����M��N���߶�FG�Ĺ��ɷָ��.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com