
【题目】计算题
(1)求值:2 ![]() sin45°+(﹣3)2﹣20170×|﹣4|+
sin45°+(﹣3)2﹣20170×|﹣4|+ ![]() ;
;
(2)先化简,再求值:( ![]() ﹣x﹣1)÷
﹣x﹣1)÷ ![]() ,其中x是不等式组
,其中x是不等式组 ![]() 的一个整数解.
的一个整数解.
【答案】
(1)解:2 ![]() sin45°+(﹣3)2﹣20170×|﹣4|+
sin45°+(﹣3)2﹣20170×|﹣4|+ ![]()
= ![]()
=2+9﹣4+6
=13;
(2)解:( ![]() ﹣x﹣1)÷
﹣x﹣1)÷ ![]()
= ![]()
= ![]()
= ![]()
=﹣(x+2)(x﹣1)
=﹣x2﹣x+2,
由 ![]() 得,﹣1<x≤2,
得,﹣1<x≤2,
∵x﹣1≠0,x﹣2≠0,
∴x≠1,x≠2,
∵x是不等式组 ![]() 的一个整数解,
的一个整数解,
∴x=0,
当x=0时,原式=﹣02﹣0+2=2
【解析】(1)根据特殊角的三角函数值、负整数指数幂、零指数幂、绝对值可以解答本题;(2)先化简题目中的式子,然后求出不等式组 ![]() 的解集,然后选取一个使得原分式有意义的整数值代入即可解答本题.
的解集,然后选取一个使得原分式有意义的整数值代入即可解答本题.
【考点精析】利用零指数幂法则和整数指数幂的运算性质对题目进行判断即可得到答案,需要熟知零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,3,4,7.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于5且小于8的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣2x+10与x轴,y轴相交于A,B两点,点C的坐标是(8,4),连接AC,BC.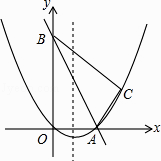
(1)求过O,A,C三点的抛物线的解析式,并判断△ABC的形状;
(2)动点P从点O出发,沿OB以每秒2个单位长度的速度向点B运动;同时,动点Q从点B出发,沿BC以每秒1个单位长度的速度向点C运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t秒,当t为何值时,PA=QA?
(3)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三角形?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
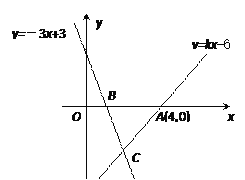
【题目】如图,直线y=kx-6经过点A(4,0),直线y=-3x+3与x轴交于点B,且两直线交于点C.
(1)求k的值.
(2)求△ABC的面积.
(3)在直线y=kx-6上是否存在异于点C的另一点P,使得△ABP与△ABC的面积相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简: ![]() (2)解方程:
(2)解方程:![]() .
.
【答案】(1) ![]() 或
或![]() ;(2)x=-2.
;(2)x=-2.
【解析】(1)先把括号内通分,再把除法转化为乘法,并把分子、分母分解因式约分化简;
(2)两边都乘以最简公分母2(x+3),把分式方程化为整式方程求解,求出x的值不要忘记检验.
(1)原式=![]() =
=![]() =
=![]() 或
或![]() ;
;
(2)解:去分母得:![]() ,
,
解得:x=﹣2,
经检验x=﹣2是分式方程的解,
∴原方程的解为x=﹣2
点睛:本题考查了分式的混合运算和解分式方程,熟练掌握分式的运算法则和解分式方程的方法是解答本题的关键.
【题型】解答题
【结束】
20
【题目】小张同学学完统计知识后,随机调查了她所在辖区若干名居民的年龄,将调查数据绘制成如下扇形统计图和条形统计图:

请根据以上不完整的统计图提供的信息,解答下列问题:
(1)小张同学共调查了 名居民的年龄,扇形统计图中a= ;
(2)补全条形统计图,并注明人数;
(3)若在该辖区中随机抽取一人,那么这个人年龄是60岁及以上的概率为 ;
(4)若该辖区年龄在0~14岁的居民约有2400人,请估计该辖区居民有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB的中点,点D在线段CB上.
![]()
(1)图中共有 条线段.
(2)图中AD=AC+CD,BC=AB﹣AC,类似地,请你再写出两个有关线段的和与差的关系式:
① ;② .
(3)若AB=8,DB=1.5,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
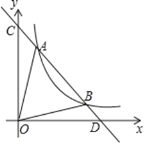
【题目】如图,一次函数![]() 分别交y轴、x轴于C、D两点,与反比例函数y=
分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求反比例函数的解析式;
(2)根据图象直接写出![]() <
<![]() 的x的取值范围;
的x的取值范围;
(3)求![]() 的面积.
的面积.
【答案】(1)y=![]() ;(2)
;(2) ![]() 或
或![]() ;(3)15.
;(3)15.
【解析】(1)把B(4,n)两点分别代入![]() 可求出n的值,确定B点坐标为B(4,2),后利用待定系数法求反比例函数的解析式;
可求出n的值,确定B点坐标为B(4,2),后利用待定系数法求反比例函数的解析式;
(2)观察函数图象得到当![]() 或
或![]() ,反比例函数的图象在一次函数图象上方.
,反比例函数的图象在一次函数图象上方.
(3)求得直线![]() 与坐标轴轴的交点坐标,根据三角形面积公式即可求得.
与坐标轴轴的交点坐标,根据三角形面积公式即可求得.
(1)将![]() 代入
代入![]() 得
得![]() ,
,
得反比例函数的关系式是![]() .
.
(2)![]() 或
或![]() ,
,
(3)![]() 点的坐标是(0,10),
点的坐标是(0,10),![]() 点的坐标是(5,0),
点的坐标是(5,0),
分别过点A、B两点作![]() 轴、
轴、![]() 轴的垂线段,
轴的垂线段,
![]() .
.
点睛:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式以及观察图象的能力.
【题型】解答题
【结束】
25
【题目】探索发现:![]() ;
;![]() ;
;![]() …根据你发现的规律,回答下列问题
…根据你发现的规律,回答下列问题
(1)![]() ,
,![]() ;
;
(2)利用你发现的规律计算:![]() ;
;
(3)灵活利用规律解方程:
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE∥BD,过点D作DE∥AC,CE与DE相交于点E.
(1)求证:四边形CODE是矩形.
(2)若AB=5,AC=6,求四边形CODE的周长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com