
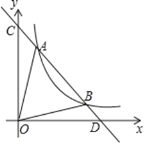
【题目】如图,一次函数![]() 分别交y轴、x轴于C、D两点,与反比例函数y=
分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求反比例函数的解析式;
(2)根据图象直接写出![]() <
<![]() 的x的取值范围;
的x的取值范围;
(3)求![]() 的面积.
的面积.
【答案】(1)y=![]() ;(2)
;(2) ![]() 或
或![]() ;(3)15.
;(3)15.
【解析】(1)把B(4,n)两点分别代入![]() 可求出n的值,确定B点坐标为B(4,2),后利用待定系数法求反比例函数的解析式;
可求出n的值,确定B点坐标为B(4,2),后利用待定系数法求反比例函数的解析式;
(2)观察函数图象得到当![]() 或
或![]() ,反比例函数的图象在一次函数图象上方.
,反比例函数的图象在一次函数图象上方.
(3)求得直线![]() 与坐标轴轴的交点坐标,根据三角形面积公式即可求得.
与坐标轴轴的交点坐标,根据三角形面积公式即可求得.
(1)将![]() 代入
代入![]() 得
得![]() ,
,
得反比例函数的关系式是![]() .
.
(2)![]() 或
或![]() ,
,
(3)![]() 点的坐标是(0,10),
点的坐标是(0,10),![]() 点的坐标是(5,0),
点的坐标是(5,0),
分别过点A、B两点作![]() 轴、
轴、![]() 轴的垂线段,
轴的垂线段,
![]() .
.
点睛:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数的解析式.也考查了待定系数法求函数的解析式以及观察图象的能力.
【题型】解答题
【结束】
25
【题目】探索发现:![]() ;
;![]() ;
;![]() …根据你发现的规律,回答下列问题
…根据你发现的规律,回答下列问题
(1)![]() ,
,![]() ;
;
(2)利用你发现的规律计算:![]() ;
;
(3)灵活利用规律解方程:
![]()
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】南昌的雾霾引起了小张对环保问题的重视.一次旅游小张思考了一个问题.从某地到南昌,若乘火车需要![]() 小时,若乘汽车需要
小时,若乘汽车需要![]() 小时.这两种交通工具平均每小时二氧化碳的排放量之和为
小时.这两种交通工具平均每小时二氧化碳的排放量之和为![]() 千克,火车全程二氧化碳的排放总量比汽车的多
千克,火车全程二氧化碳的排放总量比汽车的多![]() 千克,分别求火车和汽车平均每小时二氧化碳的排放量.
千克,分别求火车和汽车平均每小时二氧化碳的排放量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组建了书法、音乐、美术、舞蹈、演讲五个社团,全校每一名学生都参加且只参加了其中一个社团的活动.校团委从全校学生中随机选取部分学生进行了参加活动情况的调查,并将调查结果制成了如图不完整的统计图.请根据统计图完成下列问题:
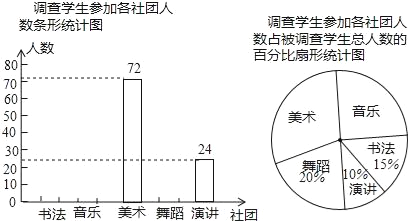
(1)参加本次调查有 名学生?
(2)根据调查数据分析,被调查的学生中有 名学生参加了音乐社团?
(3)请你补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)求值:2 ![]() sin45°+(﹣3)2﹣20170×|﹣4|+
sin45°+(﹣3)2﹣20170×|﹣4|+ ![]() ;
;
(2)先化简,再求值:( ![]() ﹣x﹣1)÷
﹣x﹣1)÷ ![]() ,其中x是不等式组
,其中x是不等式组 ![]() 的一个整数解.
的一个整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
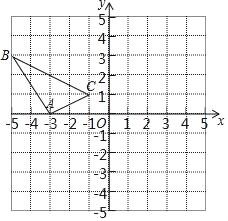
【题目】在边长为1个单位长度的小正方形组成的网格中,建立如图所示的平面直角坐标系△ABC是格点三角形(顶点在网格线的交点上)
(1)先作△ABC关于原点O成中心对称的△A1B1C1,再把△A1B1C1向上平移4个单位长度得到△A2B2C2;
(2)△A2B2C2与△ABC是否关于某点成中心对称?若是,直接写出对称中心的坐标;若不是,请说明理由.
【答案】(1)画图见解析;(2)(0,2).
【解析】
(1)根据中心对称和平移性质分别作出变换后三顶点的对应点,再顺次连接可得;
(2)根据中心对称的概念即可判断.
(1)如图所示,△A1B1C1和△A2B2C2即为所求;
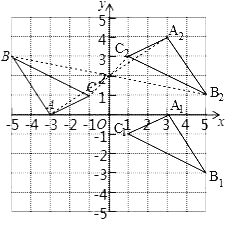
(2)由图可知,△A2B2C2与△ABC关于点(0,2)成中心对称.
点睛:本题考查了中心对称作图和平移作图,熟练掌握中心对称的性质和平移的性质是解答本题的关键. 中心对称的性质:①关于中心对称的两个图形能够完全重合;②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.
【题型】解答题
【结束】
22
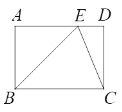
【题目】如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
(1)△BEC是否为等腰三角形?证明你的结论.
(2)已知AB=1,∠ABE=45°,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1、2、3,…是由花盆摆成的图案,图1中有1盆花,图2中有7盆花,图3中有19盆花,……
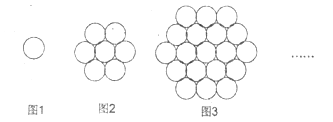
根据图中花盆摆放的规律,图4中,应该有__________盆花;第n个图形中应该有_________盆花。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.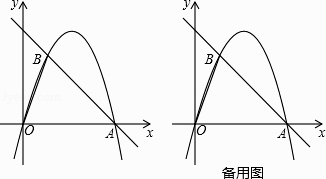
(1)求a,b的值;
(2)点P是线段AB上一动点(点P不与点A、B重合),过点P作PM//OB交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,过点P作PF⊥MC于点F,设PF的长为t,MN的长为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,当S△ACN=S△PMN时,连接ON,点Q在线段BP上,过点Q作QR//MN交ON于点R,连接MQ、BR,当∠MQR﹣∠BRN=45°时,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距2400米,甲、乙两人分别从A,B两地同时出发相向而行,乙的速度是甲的2倍,已知乙到达A地15分钟后甲到达B地.
(1)求甲每分钟走多少米?
(2)两人出发多少分钟后恰好相距480米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)-16+23+(-17)-(-7)
(2) ![]()
(3)![]()
(4)(-8)÷(![]() )-2×(-6)
)-2×(-6)
(5)![]()
(6)(-![]() )2×
)2×![]() ÷|-
÷|-![]() |+(-2)÷(
|+(-2)÷(![]() )4
)4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com