
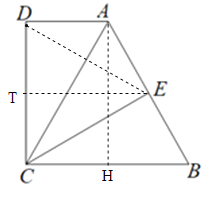
【题目】如图,四边形ABCD中,∠BCD=∠D=90°,E是边AB的中点.已知AD=1,AB=2.
(1)设BC=x,CD=y,求y关于x的函数关系式,并写出定义域;
(2)当∠B=70°时,求∠AEC的度数;
(3)当△ACE为直角三角形时,求边BC的长.

【答案】(1)![]() ;(2)∠AEC=105°;(3)边BC的长为2或
;(2)∠AEC=105°;(3)边BC的长为2或![]() .
.
【解析】试题分析:(1)过A作AH⊥BC于H,得到四边形ADCH为矩形.在△BAH中,由勾股定理即可得出结论.
(2)取CD中点T,连接TE,则TE是梯形中位线,得ET∥AD,ET⊥CD,∠AET=∠B=70°.
又AD=AE=1,得到∠AED=∠ADE=∠DET=35°.由ET垂直平分CD,得∠CET=∠DET=35°,即可得到结论.
(3)分两种情况讨论:①当∠AEC=90°时,易知△CBE≌△CAE≌△CAD,得∠BCE=30°,
解△ABH即可得到结论.
②当∠CAE=90°时,易知△CDA∽△BCA,由相似三角形对应边成比例即可得到结论.
试题解析:解:(1)过A作AH⊥BC于H.由∠D=∠BCD=90°,得四边形ADCH为矩形.
在△BAH中,AB=2,∠BHA=90°,AH=y,HB=![]() ,∴
,∴![]() ,
,
则![]()
(2)取CD中点T,联结TE,则TE是梯形中位线,得ET∥AD,ET⊥CD,∴∠AET=∠B=70°.
又AD=AE=1,∴∠AED=∠ADE=∠DET=35°.由ET垂直平分CD,得∠CET=∠DET=35°,∴∠AEC=70°+35°=105°.
(3)分两种情况讨论:①当∠AEC=90°时,易知△CBE≌△CAE≌△CAD,得∠BCE=30°,
则在△ABH中,∠B=60°,∠AHB=90°,AB=2,得BH=1,于是BC=2.
②当∠CAE=90°时,易知△CDA∽△BCA,又![]() ,
,
则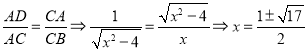 (舍负)
(舍负)
易知∠ACE<90°,所以边BC的长为![]() .
.
综上所述:边BC的长为2或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
(1)求点A,点B的坐标;
(2)求△ABC的面积;
(3)P为第二象限抛物线上的一个动点,求△ACP面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
第1个等式:a1=![]()
第2个等式:a2=![]()
第3个等式:a3=![]()
第4个等式:a4=![]()
……
请回答下列问题:
(1)按上述等式的规律,列出第5个等式:a5= =
(2)用含n的式子表示第n个等式:an= =
(3)求a1+a2+a3+a4+…+a2017的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点M,O,N对应的数分别是-1,0,3,点P为数轴上任意点,其对应的数为x.如果点P以每分钟1个单位长度的速度从点O向左运动,同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动.设t分钟时P点到点M、点N的距离相等,则t的值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:

(1)本次调查共抽查了 名学生;
(2)两幅统计图中的m= ,n= .
(3)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形。
类比研究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)。
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设![]() ,
,![]() ,
,![]() ,请探索
,请探索![]() ,
,![]() ,
,![]() 满足的等量关系。
满足的等量关系。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某风景区计划在绿化区域种植银杏树,现甲、乙两家有相同的银杏树苗可供选择,其具体销售方案如下:
甲 | 乙 | ||
购树苗数量 | 销售单价 | 购树苗数量 | 销售单价 |
不超过500棵时 | 800元/棵 | 不超过1000棵时 | 800元/棵 |
超过500棵的部分 | 700元/棵 | 超过1000棵的部分 | 600元/棵 |
设购买银杏树苗x棵,到两家购买所需费用分别为y甲元、y乙元
(1)该风景区需要购买800棵银杏树苗,若都在甲家购买所要费用为 元,若都在乙家购买所需费用为 元;
(2)当x>1000时,分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该风景区的负责人,购买树苗时有什么方案,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在△ABC中,∠C=90°,AC=BC,AB=30cm,点P在AB上,AP=10cm,点E从点P出发沿线段PA以2cm/s的速度向点A运动,同时点F从点P出发沿线段PB以1cm/s的速度向点B运动,点E到达点A后立刻以原速度沿线段AB向点B运动,在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设点E、F运动的时间为t(s)(0<t<20).
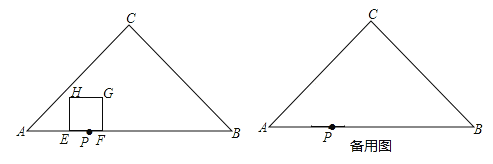
(1)当点H落在AC边上时,求t的值;
(2)设正方形EFGH与△ABC重叠部分的面积为S.①试求S关于t的函数表达式;②以点C为圆心,![]() t为半径作⊙C,当⊙C与GH所在的直线相切时,求此时S的值.
t为半径作⊙C,当⊙C与GH所在的直线相切时,求此时S的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com