Question

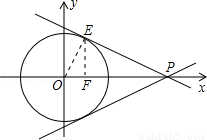
（12分）如图，已知平面直角坐标系中，⊙O的圆心在坐标原点，直线l与轴相交于点P，与⊙O相交于A、B两点，∠AOB=90°．点A和点B的横坐标是方程的两根，且两根之差为3．

（1）求方程的两根；

（2）求A、B两点的坐标及⊙O的半径；

（3）把直线l绕点P旋转，使直线l与⊙O相切，求直线l的解析式．

 

Answer 1

（1）2和－1；（2）A（﹣1，2），B（2，1），；（3）或．

【解析】

试题分析：（1）设方程的两根分别为，根据点A和点B的横坐标是方程的两根，且两根之差为3列出方程组，再求解即可；

（2）过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，先证出△AOC≌△OBD，求出BD=OC=1，AC=OD=2，再求出点A、B的坐标，即可求出OA，

（3）设直线AB的解析式为，求出，当时，求出P的坐标，当直线l与⊙O的切点在第一象限时，设直线l与⊙O相切于点E，过点E作EF⊥x轴于点F，根据OE⊥PE，求出PE，根据S△POE=OP•EF=OE•PE，求出EF，从而得出OF=1，E（1，2），设直线l的解析式为，则，求出，当直线l与⊙O的切点在第四象限时，同理可求得．

试题解析：（1）设方程的两根分别为，由已知得：，解得，则方程的两根分别为2和﹣1；

（2）过点A作AC⊥x轴于点C，过点B作BD⊥x轴于点D，

在△AOC和△OBD中，∵∠BDO=∠OCA，∠BOD=∠OAC，OA=OB，∴△AOC≌△OBD（AAS）

∴BD=OC=1，AC=OD=2，∴A（﹣1，2），B（2，1），

∴OA=，

（3）设直线AB的解析式为，则，解得，∴，

当时，，解得，∴P（5，0），

当直线l与⊙O的切点在第一象限时，设直线l与⊙O相切于点E，过点E作EF⊥x轴于点F，

∵PE是⊙O的切线，∴OE⊥PE，∴PE=，

∵S△POE=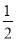OP•EF=OE•PE，∴5EF=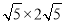，∴EF=2，∴OF==1，E（1，2），

设直线l的解析式为，则，解得，∴，

当直线l与⊙O的切点在第四象限时，同理可求得．

考点：圆的综合题．