练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．2016年11月10日，记者从民政部召开的会议了解到，目前全国农村留守儿童数量为902万人，“902万”用科学记数法表示为（　　）
    A．9.02×102B．9.02×105C．9.02×106D．9.02×104

    分析 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

    解答 解：将902万用科学记数法表示为：9.02×106．
    故选：C．

    点评 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    18．先化简，再求值：2x2-[3（-$\frac{1}{3}$x2+$\frac{2}{3}$xy）-2y2]-2（x2-xy+2y2），其中x=$\frac{1}{2}$，y=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．下列运算正确的是（　　）
    A．x3•x5=x15B．（x2）5=x7C．$\root{3}{27}$=3D．$\frac{-a+b}{a+b}$=-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．计算：$\sqrt{\frac{4}{9}}$=$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知二次函数y=5x2-12x+7．
    （1）求自变量x=1时的函数值；
    （2）求该二次函数的图象与x轴公共点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

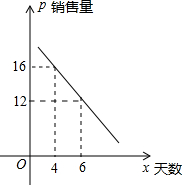    13．某水果店新进一种水果，进价为20元/盒，为了摸清行情，决定试营销10天，商家通过这10天的市场调查发现：
    ①销售价y（元/盒）与销售天数x（天）满足以下关系：
     天数 1≤x≤5 6≤x≤10
     销售价格y $\frac{1}{2}$x+24 30
    ②每天的销售量p（盒数）与销售天数x关系如图所示．
    （1）试求每天的销售量p（盒数）与销售天数x之间函数关系式；
    （2）设水果店的销售利润为s（元），求销售利润s（元）与销售天数x（天）之间的函数关系式，并求出试营销期间一天的最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．一个数的平方等于这个数的三倍这个数是0或3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．抛物线y=-x2+2x+3与x轴相交与A、B两点，与y轴相交于C，顶点D
    （1）直接写出三A、B、C点的坐标和抛物线的对称轴．
    （2）连接BC与抛物线的对称轴交与E点，P为线段BE上一点，过点P作直线PF平行于y轴交抛物线于点F，设P点的横坐标为m．
    ①用含m的代数式表示线段PF的长，并求出当m为何值时，以点P、E、D、F为顶点的四边形为平行四边形．
    ②在①的条件下，求△BCF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

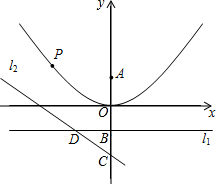    2．如图，在平面直角坐标系中，直线l1过点B（0，-1），且平行于x轴，直线l2过点C（0，-2），交直线l1于点D，$\frac{BD}{BC}=\frac{4}{3}$，点A与点B关于x轴对称，点P为抛物线y=$\frac{1}{4}$x2上一动点，PQ⊥l1于点Q．
    （1）求直线l2的函数关系式；
    （2）连接PA，AQ，OD，是否存在点P，使△PAQ与△OCD相似，若存在，求出点P坐标；若不存在，请说明理由；
    （3）当点P到直线l1与直线l2的距离之和最短时，求出点P坐标及最短距离．

    查看答案和解析>>

    同步练习册答案