
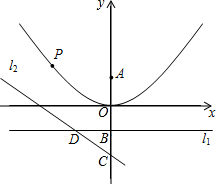
 如图,在平面直角坐标系中,直线l1过点B(0,-1),且平行于x轴,直线l2过点C(0,-2),交直线l1于点D,$\frac{BD}{BC}=\frac{4}{3}$,点A与点B关于x轴对称,点P为抛物线y=$\frac{1}{4}$x2上一动点,PQ⊥l1于点Q.
如图,在平面直角坐标系中,直线l1过点B(0,-1),且平行于x轴,直线l2过点C(0,-2),交直线l1于点D,$\frac{BD}{BC}=\frac{4}{3}$,点A与点B关于x轴对称,点P为抛物线y=$\frac{1}{4}$x2上一动点,PQ⊥l1于点Q.分析 (1)先求出BC的长,进而求出BD,即可得出点D坐标,利用待定系数法确定出直线l2的解析式;
(2)先利用两点间的距离求出PA,PQ进而得出PA=PQ,即可得出∠DOC=∠DCO,再用△PAQ与△OCD相似得出$\frac{BD}{BQ}=\frac{BO}{BA}$即可得出结论;
(3)先判断出点P到直线l1与直线l2的距离之和最短时,点P的位置,利用相似三角形得出的比例式求出AM,联立成方程组求出点P的坐标.
解答 解:(1)∵B(0,-1),C(0,-2),
∴BC=1,
∵$\frac{BD}{BC}=\frac{4}{3}$,
∴BD=$\frac{4}{3}$,
∴D点坐标为($-\frac{4}{3}$,-1).
设直线l2为y=kx+b,
∴$\left\{\begin{array}{l}-\frac{4}{3}k+b=-1\\ b=-2.\end{array}\right.$,
∴$\left\{\begin{array}{l}k=-\frac{3}{4}\\ b=-2.\end{array}\right.$,
∴直线l2的解析式为$y=-\frac{3}{4}x-2$.
(2)存在.
如图1,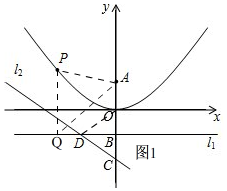
设点P为(x,$\frac{1}{4}{x^2}$),由已知得A(0,1),
∴PA2=${x^2}+{(\frac{1}{4}{x^2}-1)^2}$=$\frac{1}{16}{x^4}+\frac{1}{2}{x^2}+1$,PQ2=${(\frac{1}{4}{x^2}+1)^2}$=$\frac{1}{16}{x^4}+\frac{1}{2}{x^2}+1$,
∴PA2=PQ2,即PA=PQ,
∴∠PQA=∠PAQ.
∵OB=BC=1,BD⊥OC,
∴OD=CD,
∴∠DOC=∠DCO,
∴要使△PAQ与△OCD相似,有且只有∠PQA=∠DOC.
∵∠PQA+∠AQB=∠ODB+∠DOC=90°,
∴∠AQB=∠ODB,
∴△AQB∽△ODB,
∴$\frac{BD}{BQ}=\frac{BO}{BA}$.
∵BD=$\frac{4}{3}$,BO=1,BA=2,
∴BQ=$\frac{8}{3}$,
∴x=$±\frac{8}{3}$,
∴点P为($\frac{8}{3}$,$\frac{16}{9}$)或($-\frac{8}{3}$,$\frac{16}{9}$).
(3)如图2,
由(2)可知PA=PQ,
∴点P到直线l1与直线l2的距离之和即为点P到点A与直线l2的距离之和,
∴过点A作AM⊥直线l2于点M,
点P到直线l1与直线l2的最短距离之和为线段AM的长,AM与抛物线交点,即为所求点P,
此时,由△AMC∽△DBC得AM=$\frac{12}{5}$
∵直线l2的解析式为$y=-\frac{3}{4}x-2$.A(0,1)
直线AM的解析式为$y=\frac{4}{3}x+1$①,
∵点P为抛物线y=$\frac{1}{4}$x2②上,
联立①②得,P($-\frac{2}{3}$,$\frac{1}{9}$)(另一点(6,9)舍去)
当点P到直线l1与直线l2的距离之和最短时,
点P坐标为($-\frac{2}{3}$,$\frac{1}{9}$),最短距离为$\frac{12}{5}$.
点评 此题二次函数综合题,主要考查了待定系数法,相似三角形的性质和判定,极值问题,方程组的解法,解(1)的关键利用待定系数法确定函数解析式,解(2)的关键是判断出∠DOC=∠DCO,解(3)的关键确定出点P的位置和解方程组;是一道中等难度的中考常考题.


科目:初中数学 来源: 题型:选择题
| A. | 9.02×102 | B. | 9.02×105 | C. | 9.02×106 | D. | 9.02×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
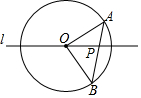 如图,已知点A、B为⊙O上的两点,且∠A=40°,直线l经过圆心O,与AB相交于点P,若直线l绕点O旋转,当△OBP为等腰三角形时,∠AOP=60°.
如图,已知点A、B为⊙O上的两点,且∠A=40°,直线l经过圆心O,与AB相交于点P,若直线l绕点O旋转,当△OBP为等腰三角形时,∠AOP=60°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a<1 | B. | a≤1 | C. | a<0 | D. | a≤0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①④ | B. | ①② | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com