
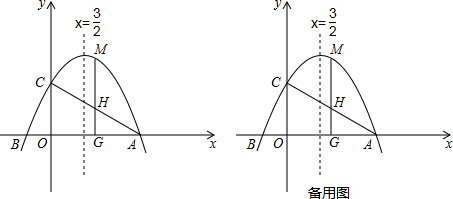
分析 (1)首先利用对称轴公式求出a的值,然后把点A的坐标与a的值代入抛物线的解析式,求出c的值,即可确定出抛物线的解析式.
(2)首先根据抛物线的解析式确定出点C的坐标,再根据待定系数法,确定出直线AC解析式为y=-$\frac{1}{2}$x+2;然后设点M的坐标为(m,-$\frac{1}{2}$m2+$\frac{3}{2}$m+2),H(m,-$\frac{1}{2}$m+2),求出MH的值是多少,再根据CM=CH,OC=GE=2,可得MH=2EH,据此求出m的值是多少,再把m的值代入抛物线的解析式,求出y的值,即可确定点M的坐标.
(3)首先判断出△ABC为直角三角形,然后分两种情况:①当$\frac{{N}_{1}{P}_{1}}{AC}$=$\frac{{P}_{1}G}{CB}$时;②当$\frac{{N}_{2}{P}_{2}}{BC}$=$\frac{{P}_{2}G}{CA}$时;根据相似三角形的性质,判断出是否存在点P,使得以P、N、G为顶点的三角形与△ABC相似即可.
解答 解:(1)∵x=-$\frac{b}{2a}$=$\frac{3}{2}$,b=$\frac{3}{2}$,
∴a=-$\frac{1}{2}$,
把A(4,0),a=-$\frac{1}{2}$代入y=ax2+$\frac{3}{2}$x+c,
可得($-\frac{1}{2}$)×42+$\frac{3}{2}$×4+c=0,
解得c=2,
则抛物线解析式为y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2.
(2)如图1,连接CM,过C点作CE⊥MH于点E,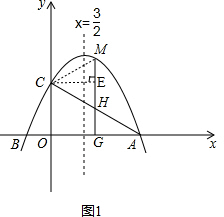 ,
,
∵y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2,
∴当x=0时,y=2,
∴C点的坐标是(0,2),
设直线AC解析式为y=kx+b(k≠0),
把A(4,0)、C(0,2)代入y=kx+b,
可得$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线AC解析式为y=-$\frac{1}{2}$x+2,
∵点M在抛物线上,点H在AC上,MG⊥x轴,
∴设点M的坐标为(m,-$\frac{1}{2}$m2+$\frac{3}{2}$m+2),H(m,-$\frac{1}{2}$m+2),
∴MH=-$\frac{1}{2}$m2+$\frac{3}{2}$m+2-(-$\frac{1}{2}$m+2)=-$\frac{1}{2}$m2+2m,
∵CM=CH,OC=GE=2,
∴MH=2EH=2×[2-(-$\frac{1}{2}$m+2)]=m,
又∵MH=-$\frac{1}{2}$m2+2m,
∴-$\frac{1}{2}$m2+2m=m,
即m(m-2)=0,
解得m=2或m=0(不符合题意,舍去),
∴m=2,
当m=2时,
y=-$\frac{1}{2}$×22+$\frac{3}{2}$×2+2=3,
∴点M的坐标为(2,3).
(3)存在点P,使以P,N,G为顶点的三角形与△ABC相似,理由为:
∵抛物线与x轴交于A、B两点,A(4,0),A、B两点关于直线x=$\frac{3}{2}$成轴对称,
∴B(-1,0),
∵AC=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,BC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,AB=5,
∴AC2+BC2=${(2\sqrt{5})}^{2}$+${(\sqrt{5})}^{2}$=25,AB2=52=25,
∵AC2+BC2=AB2=25,
∴△ABC为直角三角形,
∴∠ACB=90°,
线段MG绕G点旋转过程中,与抛物线交于点N,当NP⊥x轴时,∠NPG=90°,
设P点坐标为(n,0),
则N点坐标为(n,-$\frac{1}{2}$n2+$\frac{3}{2}$n+2),
①如图2,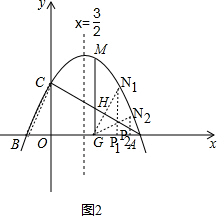
当$\frac{{N}_{1}{P}_{1}}{AC}$=$\frac{{P}_{1}G}{CB}$时,
∵∠N1P1G=∠ACB=90°,
∴△N1P1G∽△ACB,
∴$\frac{-\frac{1}{2}{n}^{2}+\frac{3}{2}n+2}{2\sqrt{5}}$=$\frac{n-2}{\sqrt{5}}$,
解得:n1=3,n2=-4(不符合题意,舍去),
∴P的坐标为(3,0).
②当$\frac{{N}_{2}{P}_{2}}{BC}$=$\frac{{P}_{2}G}{CA}$时,
∵∠N2P2G=∠BCA=90°,
∴△N2P2G∽△BCA,
∴$\frac{-{\frac{1}{2}n}^{2}+\frac{3}{2}n+2}{\sqrt{5}}=\frac{n-2}{2\sqrt{5}}$,
解得:n1=1$+\sqrt{7}$,n2=1-$\sqrt{7}$(不符合题意,舍去),
∴P的坐标为(1+$\sqrt{7}$,0).
∴存在点P(3,0)或(1$+\sqrt{7}$,0),使以P,N,G为顶点的三角形与△ABC相似.
点评 (1)此题主要考查了二次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了待定系数法求函数解析式的方法,要熟练掌握.
(3)此题还考查了相似三角形的性质和应用,以及直角三角形的性质和应用,要熟练掌握.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②当AD=2时,EF与半圆相切;③线段EF的最小值为4;④若点F恰好落在BC上,则AD=4.其中正确结论的序号是①②.
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②当AD=2时,EF与半圆相切;③线段EF的最小值为4;④若点F恰好落在BC上,则AD=4.其中正确结论的序号是①②.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{2}{5}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{4}{7}$ | D. | -$\frac{2}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com