
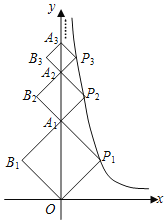
【题目】如图,四边形OP1A1B1,A1P2A2B2,A2P3A3B3,An﹣1PnAnBn都是正方形,其中点A1、A2、A3…An在y轴上,点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)在反比例函数y=![]() (x>0)的图象上,已知B1(﹣1,1),则点Pn的坐标为( )
(x>0)的图象上,已知B1(﹣1,1),则点Pn的坐标为( )
A.![]() B.
B.![]()
C.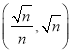 D.
D.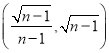
【答案】A
【解析】
由四边形OP1A1B1为正方形且OA1是对角线知B1与P1关于y轴对称,得出点P1(1,1),由点P1坐标及正方形的性质知OA1=2,据此可设P2的坐标为(a,a+2),代入解析式求得a的值即可,同理可得点P3的坐标,根据P1、P2,P3的坐标得规律:知点Pn的坐标为(![]() ﹣
﹣![]() ,
,![]() +
+ ![]() ).
).
解:在正方形OP1A1B1中,OA1是对角线,
则B1与P1关于y轴对称,
∵B1(﹣1,1),
∴P1(1,1),
则k=1×1=1,即反比例函数解析式为y=![]() ;
;
设P2(a,a+2),代入y=![]() ,
,
∴a(a+2)=1,
∴a=﹣1±![]() ,
,
∵a>0,
∴a=![]() ﹣1,
﹣1,
∴P2(![]() ﹣1,
﹣1,![]() +1),
+1),
设P3(b,b+2 ![]() ),代入y=
),代入y=![]() ,
,
∴b(b+2 ![]() )=1,
)=1,
∴b=﹣![]() ±
±![]() ,
,
∵b>0,
∴b=![]() ﹣
﹣![]() ,
,
P3(![]() ﹣
﹣![]() ,
,![]() +
+ ![]() ),
),
……
∴Pn的坐标为(![]() ﹣
﹣![]() ,
,![]() +
+ ![]() ).
).
故选:A.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】小亮、小芳和两个陌生人甲、乙同在如图所示的地下车库等电梯,已知两个陌生人到1至4 层的任意一层出电梯,并设甲在a层出电梯,乙在b层出电梯.
(1)请你用画树状图或列表法求出甲、乙二人在同一层楼出电梯的概率;
(2)小亮和小芳打赌说:“若甲、乙在同一层或相邻楼层出电梯,则小亮胜,否则小芳胜”.该游戏是否公平?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC.
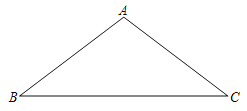
(1)用无刻度的直尺和圆规作△ABC的外接圆;(保留画图痕迹)
(2)若AB=10,BC=16,求△ABC的外接圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
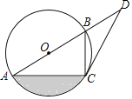
【题目】如图,已知AB是⊙O的直径,C是⊙O上的点,点D在AB的延长线上,∠BCD=∠BAC.
(1)求证:CD是⊙O的切线.
(2)若∠D=30°,BD=2,求⊙O的半径
(3)在(2)的条件下,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现将标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌子上,所有卡片的形状、大小都完全相同.现随机从中抽取一张卡片将其上面的数字作为十位上的数,然后放回洗匀,再随机抽取一张卡片,将其上面的数字作为个位上的数,组成两位数.
(1)请用列表或画树状图的方法表示出所有可能出现的结果:
(2)求这个两位数恰好能被3整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E与点F分别在线段AC、BC上,且四边形DEFG是正方形。
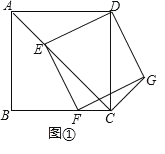
(1)求证AE=CG,并说明理由。
(2)连接AG,若AB=17,DG=13,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为8元的商品,经调研发现,这种商品每天的销售量y(件)是关于销售单价x(元)的一次函数,其关系如下表:
x(元) | 10 | 11 | 12 | 13 | 14 |
y(件) | 100 | 90 | 80 | 70 | 60 |
(1)求y与x之间的关系式;
(2)设商店每天销售利润为w(元),求出w与x之间的关系式,并求出每天销售单价定为多少时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】斗门某养殖户每年的养殖成本包括固定成本和可变动成本,其中固定成本每年均为4万元,可变动成本逐年增长. 已知该养殖户第1年的可变动成本为2万元,设可变动成本的年平均增长率为x.
(1)用含x的代数式表示第2年的可变动成本: 万元;
(2)如果该养殖户第3年的成本为6.42万元,求可变动成本的年平均增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
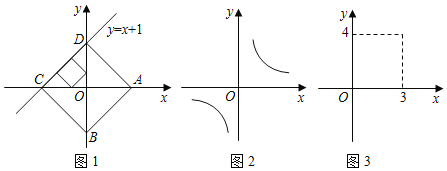
【题目】已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A.B.C.D各点依次排列)为正方形时,我们称这个正方形为此函数图象的“和谐正方形”.例如:在图1中,正方形ABCD是一次函数y=x+1图象的其中一个“和谐正方形”.
(1)如图1,若某函数是一次函数y=x+1,求它的图象的所有“和谐正方形”的边长;
(2)如图2,若某函数是反比例函数y=![]() (k>0),它的图象的“和谐正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;
(k>0),它的图象的“和谐正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;
(3)如图3,若某函数是二次函数y=ax2+c(a≠0),它的图象的“和谐正方形”为ABCD,C、D中的一个点坐标为(3,4),请求出该二次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com