
【题目】某商场用2730元购进A、B两种新型节能日光灯共60盏,这两种日光灯的进价、标价如下表所示.

(1)这两种日光灯各购进多少盏?
(2)若A型日光灯按标价的9折出售,要使这批日光灯全部售出后商场获得810元的利润,则B型日光灯应按标价的几折出售?
【答案】(1)A 39 B 21 ;(2)八五折
【解析】试题分析:(1)设购进A型台灯x盏.则购进B型日光灯(60-x)盏,则购买A型灯钱数+购买B型灯钱数=2730.
(2)根据利润=售价-进价,知商场共获利=A型灯利润+B型灯利润,列方程求解即可.
试题解析:(1)设购进A型节能日光灯x盏.
35x+65(60-x)=2730,
解得,x=39,
60-39=21(盏)
答:购进A型节能日光灯39盏,B型节能日光灯21盏.
(2)设B型日光灯应按标价的x折出售,根据题意得:
39×(0.9×50-35)+21×(x%×100-65)=810,
解得:x=85.
故B型日光灯应按标价的八五折出售.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知:如图1,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).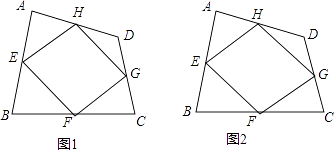
(1)四边形EFGH的形状是 , 证明你的结论.
(2)如图2,请连接四边形ABCD的对角线AC与BD,当AC与BD满足条件时,四边形EFGH是矩形;证明你的结论.
(3)你学过的哪种特殊四边形的中点四边形是矩形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①若a与c相交,b与c相交,则a与b相交;②若a//b,b//c,那么a//c;③经过直线外一点有且只有一条直线与已知直线平行;④两条直线的位置关系有平行与相交.
其中错误的说法有( )
A. 3个B. 2个C. 1个D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中是随机事件的个数是( )
①投掷一枚硬币,正面朝上;
②五边形的内角和是540°;
③20件产品中有5件次品,从中任意抽取6件,至少有一件是次品;
④一个图形平移后与原来的图形不全等.
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com