
分析 (1)根据二次根式的性质化简即可;
(2)先把原式化为完全平方的形式,根据二次根式的性质化简;
(3)把原式化为完全平方的形式,根据二次根式的性质化简.
解答 解:(1)$\sqrt{5-2\sqrt{6}}$=$\sqrt{({\sqrt{3})}^{2}-2×\sqrt{3}×\sqrt{2}+(\sqrt{2})^{2}}$=$\sqrt{({\sqrt{3}-\sqrt{2})}^{2}}$=$\sqrt{3}-\sqrt{2}$;
$\sqrt{12+2\sqrt{35}}$=$\sqrt{(\sqrt{7}+\sqrt{5})^{2}}$=$\sqrt{7}$+$\sqrt{5}$;
故答案为:$\sqrt{3}-\sqrt{2}$;$\sqrt{7}$+$\sqrt{5}$;
(2)①$\sqrt{9+6\sqrt{2}}$=$\sqrt{9+2\sqrt{18}}$=$\sqrt{6+2×\sqrt{6}×\sqrt{3}+3}$=$\sqrt{({\sqrt{6}+\sqrt{3})}^{2}}$=$\sqrt{6}$+$\sqrt{3}$;
②$\sqrt{16-4\sqrt{15}}$=$\sqrt{10-2\sqrt{10}×\sqrt{6}+6}$=$\sqrt{(\sqrt{10}-\sqrt{6})^{2}}$=$\sqrt{10}$-$\sqrt{6}$;
(3)$\sqrt{3-\sqrt{5}}+\sqrt{2+\sqrt{3}}$=$\sqrt{({\frac{\sqrt{10}}{2}-\frac{\sqrt{2}}{2})}^{2}}$+$\sqrt{(\frac{\sqrt{6}}{2}+\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{10}}{2}+\frac{\sqrt{6}}{2}$.
点评 本题考查的是二次根式的性质和化简,掌握二次根式的性质:$\sqrt{{a}^{2}}$=|a|和完全平方公式是解题的关键.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:选择题
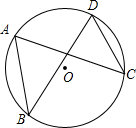 如图,A,B,C,D是⊙O上的四点,如果∠ABD与∠ACD的平分线的交点为P,则点P与⊙O的位置关系是( )
如图,A,B,C,D是⊙O上的四点,如果∠ABD与∠ACD的平分线的交点为P,则点P与⊙O的位置关系是( )| A. | 在⊙O上 | B. | 在⊙O内 | C. | 在⊙O外 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
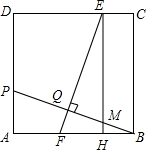 如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b<a<c | B. | b<c<a | C. | c<b<a | D. | a<c<b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com