

分析 应用:(1)由AAS证明△AOF≌△EOB,得出OF=OB,AO是△ABF的中线,即可得出结论;
(2)△AOE和△DOE是“友好三角形”,即可得到E是AD的中点,则可以求得△ABE和梯形ABCD的面积的面积,根据S四边形CDOF=S矩形ABCD-2S△ABF即可求解.
拓展:画出符合条件的两种情况:①求出四边形A′DCB是平行四边形,求出BC和A′D推出∠ACB=90°,根据三角形面积公式求出即可;②求出高CQ,求出△A′DC的面积.即可求出△ABC的面积
解答 (1)证明:∵AD∥BC,
∴∠OAF=∠OEB,
在△AOF和△EOB中,$\left\{\begin{array}{l}{∠OAF=∠OEB}&{\;}\\{∠AOF=∠EOB}&{\;}\\{AF=BE}&{\;}\end{array}\right.$,
∴△AOF≌△EOB(AAS),
∴OF=OB,
则AO是△ABF的中线.
∴△AOB和△AOF是“朋友三角形”;
(2)解:∵△AOF和△DOF是“朋友三角形”,
∴S△AOF=S△DOF,
∵△AOF≌△EOB,
∴S△AOB=S△EOB,
∵△AOB和△AOF是“朋友三角形”
∴S△AOB=S△AOF,
∴S△AOF=S△DOF=S△AOB=S△EOB,=$\frac{1}{2}$×4×2=4,
∴四边形CDOE 的面积=S梯形ABCD-2S△ABE=$\frac{1}{2}$×(4+6)×4-2×4=12;
拓展:解:分为两种情况:①如图1所示: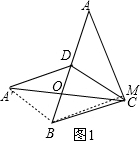
∵S△ACD=S△BCD.
∴AD=BD=$\frac{1}{2}$AB=4,
∵沿CD折叠A和A′重合,
∴AD=A′D=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
∵△A′CD与△ABC重合部分的面积等于△ABC面积的$\frac{1}{4}$,
∴S△DOC=$\frac{1}{4}$S△ABC=$\frac{1}{2}$S△BDC=$\frac{1}{2}$S△ADC=$\frac{1}{2}$S△A′DC,
∴DO=OB,A′O=CO,
∴四边形A′DCB是平行四边形,
∴BC=A′D=4,
过B作BM⊥AC于M,
∵AB=8,∠BAC=30°,
∴BM=$\frac{1}{2}$AB=4=BC,
即C和M重合,
∴∠ACB=90°,由勾股定理得:AC=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$×BC×AC=$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$;
②如图2所示: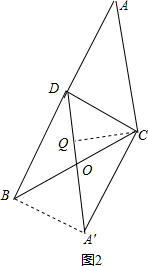 ∵S△ACD=S△BCD.
∵S△ACD=S△BCD.
∴AD=BD=$\frac{1}{2}$AB,
∵沿CD折叠A和A′重合,
∴AD=A′D=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
∵△A′CD与△ABC重合部分的面积等于△ABC面积的$\frac{1}{4}$,
∴S△DOC=$\frac{1}{4}$S△ABC=$\frac{1}{2}$S△BDC=$\frac{1}{2}$S△ADC=$\frac{1}{2}$S△A′DC,
∴DO=OA′,BO=CO,
∴四边形A′BDC是平行四边形,
∴A′C=BD=4,
过C作CQ⊥A′D于Q,
∵A′C=4,∠DA′C=∠BAC=30°,
∴CQ=$\frac{1}{2}$A′C=2,
∴S△ABC=2S△ADC=2S△A′DC=2×$\frac{1}{2}$×A′D×CQ=2×$\frac{1}{2}$×4×2=8;
即△ABC的面积是8或8$\sqrt{3}$;
故答案为:8或8$\sqrt{3}$.
点评 此题是几何变换综合题,主要考查了平行四边形性质和判定,三角形的面积,勾股定理的应用,解这个题的关键是能根据已知题意和所学的定理进行推理.题目比较好,但是有一定的难度.


科目:初中数学 来源: 题型:选择题
| A. | 点P在⊙O上 | B. | 点P在⊙O内 | C. | 点P在⊙O外 | D. | 点P不在⊙O上 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD边长为2,AB∥x轴,AD∥y轴,顶点A恰好落在双曲线y=$\frac{1}{2x}$上,边CD,BC分别交双曲线于E,F两点,若线段AE过原点,则EF的长为( )
如图,正方形ABCD边长为2,AB∥x轴,AD∥y轴,顶点A恰好落在双曲线y=$\frac{1}{2x}$上,边CD,BC分别交双曲线于E,F两点,若线段AE过原点,则EF的长为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{\sqrt{13}}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 解分式必定产生增根 | |
| B. | 若分式方程的根是零,则必定是增根 | |
| C. | 解分式方程必须验根 | |
| D. | x=3是方程$\frac{x}{x-3}$=2+$\frac{3}{x-3}$的根 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 百分位 | B. | 个位 | C. | 千位 | D. | 十万位 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com