
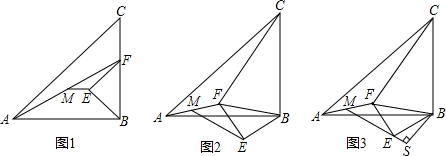
分析 (1)延长EF交AB于D,如图1,则可判断△BED和△BEF为全等的等腰直角三角形,先证明ME为△FAD的中位线得到AD=2ME,再利用等腰直角三角形的性质和等量代换得到AD=CF,于是有CF=2ME;
(2)延长FE到点G,使EG=EF,如图2,连结AG、BG,先证明ME为△FAG的中位线得到AG=2ME,然后证明△ABG≌△CBF得到AG=CF,所以CF=2ME;
(3)如图3中,作FH⊥EM于H.易证△EFH≌△BES,推出FH=ES,求出ES、EM即可解决问题;
解答 (1)证明:延长EF交AB于D,如图1,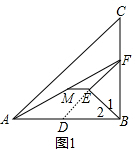
∵等腰直角△ABC和等腰直角△BEF,∠ABC=∠BEF=90°,
∴∠1=∠BFE=45°,
∴∠2=∠BDE=45°,
∴EF=ED=BE,
即BE垂直平分DF,
∵M点为AF的中点
而EF=ED,
∴ME为△FAD的中位线,
∴AD=2ME,
∵BD=BF,BA=BC,
∴AD=CF,
∴CF=2ME;
(2)解:中的结论仍成立.理由如下:
延长FE到点G,使EG=EF,如图2,连结AG、BG,
∵M点为AF的中点,
而EF=EG,
∴ME为△FAG的中位线,
∴AG=2ME,
∵△BEF为等腰直角三角形,
∴∠BEF=90°,BE=EF,
而EF=EG,
∴△BEG为等腰直角三角形,
∴∠BGE=∠EBG=45°,
∴△FBG为等腰直角三角形,
∴BF=BG,∠FBG=90°,
∵∠ABG+∠ABF=90°,∠CBF+∠ABF=90°,
∴∠ABG=∠CBF,
在△ABG和△CBF中
$\left\{\begin{array}{l}{BA=BC}\\{∠ABG=∠CBF}\\{BG=BF}\end{array}\right.$,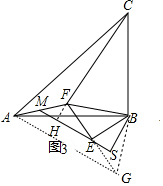
∴△ABG≌△CBF,
∴AG=CF,
∴CF=2ME;
(3)解:如图作FH⊥EM于H.易证△EFH≌△BES,
∴FH=ES,
∵BF=$\sqrt{10}$,BE=EF,∠BEF=90°,
∴BE=EF=$\sqrt{5}$,
∵BS=$\sqrt{3}$,
∴FH=ES=$\sqrt{B{E}^{2}-B{S}^{2}}$=$\sqrt{2}$,
∵CF=2EM,
∴EM=3,
∴S△EMF=$\frac{1}{2}$•EM•FH=$\frac{1}{2}$•3•$\sqrt{2}$=$\frac{3\sqrt{2}}{2}$.
点评 本题考查了几何变换综合题:熟练掌握旋转的性质和等腰直角三角形的性质;利用线段中点构建三角形中位线得到线段之间的位置关系与数量关系;会利用全等三角形的知识解决线段相等的问题.


科目:初中数学 来源: 题型:解答题
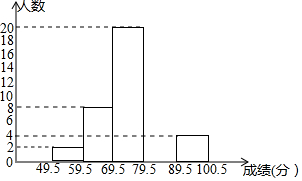 某校数学兴趣小组成员刘明对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析(每个人的成绩各不相同),绘制成如下下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:
某校数学兴趣小组成员刘明对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析(每个人的成绩各不相同),绘制成如下下频数分布表和频数分布直方图,请你根据图表提供的信息,解答下列问题:| 分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~100.5 | 合计 |
| 频数 | 2 | 8 | 20 | a | 4 | c |
| 频率 | 0.04 | b | 0.40 | 0.32 | 0.08 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
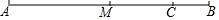 已知:如图,点M是长度为18cm的线段AB的中点,点C把线段MB分成MC:CB=2:1的两部分,求线段AC的长.
已知:如图,点M是长度为18cm的线段AB的中点,点C把线段MB分成MC:CB=2:1的两部分,求线段AC的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com