
【题目】已知直线l1:y1=x+m与直线l2:y2=nx+3相交于点A(1,2).
(1)求m、n的值;
(2)设l1交x轴于点B,l2交x轴于点C,若点D与点A,B,C能构成平行四边形,请直接写出D点坐标;
(3)请在所给坐标系中画出直线l1和l2 , 并根据图象回答问题:
当x满足时,y1>2;
当x满足时,0<y2≤3;
当x满足时,y1<y2 .
【答案】
(1)解:将点A(1,2)代入y1=x+m与y2=nx+3得2=1+m,2=n+3,
解得 m=1,n=﹣1
(2)解:由直线l1:y1=x+1与直线l2:y2=﹣x+3可知:l1交x轴于点B(﹣1,0),l2交x轴于点C(3,0),如图:
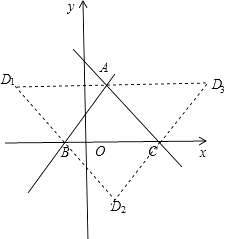
∵点D与点A,B,C能构成平行四边形,
∴D的坐标为(5,2)或(﹣3,2)或(1,﹣2)
(3)x>1,0≤x<3,x<1.
【解析】(1)将点A(1,2)的坐标分别代入两函数解析式,解方程求解,即可求出m、n的值。
(2)作出图形可知,点D与点A,B,C能构成平行四边形,即可得出点D的坐标。
(3)观察函数图像即可求解。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法),还要掌握平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中, ![]() C=2
C=2 ![]() B,点D是BC上一点,AD=6,且AD
B,点D是BC上一点,AD=6,且AD ![]() AB,点E是BD上的点,AE=
AB,点E是BD上的点,AE= ![]() BD,AC=5,贝AB的长度为 .
BD,AC=5,贝AB的长度为 . 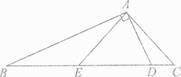
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A的坐标为(﹣2,3),则点A关于y轴的对称点的坐标是( )
A. (﹣2,3) B. (2,3) C. (2,﹣3) D. (﹣2,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是根据宝塔山公园的平面示意图建立的平面直角坐标系,公园的入口位于坐标原点O,古塔位于点A(﹣400,300),从古塔出发沿射线OA方向前行300m是盆景园B,从盆景园B向右转90°后直行400m到达樱花园C,则点C的坐标是 . 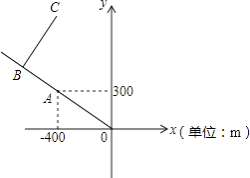
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°.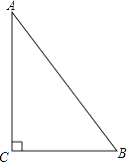
(1)在BC边上作一点P,使得点P到点C的距离与点P到边AB的距离相等(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=8,BC=6,求CP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解大气污染情况,某学校兴趣小组搜集了20I7年上半年中120天郑州市的空气质量指数,绘制了如下不完整的统计图表:
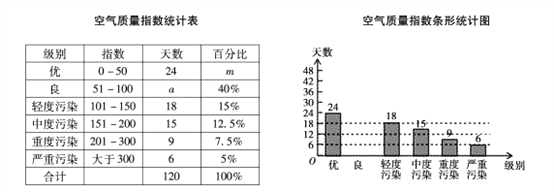
请根据图表中提供的信息,解答下面的问题:
(1)空气质量指数统计表中的a=_________,m=_________;
(2)请把空气质量指数条形统计图补充完整;
(3)若绘制“空气质量指数扇形统计图”,级别为“优”所对应扇形的圆心角是_________。
(4)请通过计算估计郑州市2017年(365)天冲空气质量指数大于100的天数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)设![]() ,求该抛物线的解析式;
,求该抛物线的解析式;
(2)在⑴中,若点![]() 为直线
为直线![]() 下方抛物线上一动点,当⊿
下方抛物线上一动点,当⊿![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
(3)是否存在整数![]() 使得
使得![]() 和
和![]() 同时成立,请证明你的结论.
同时成立,请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com