
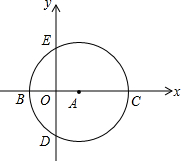
 ��ͼ����ֱ������ϵ�У��Ե�A��3��0��ΪԲ�ģ���5Ϊ�뾶��Բ��x���ཻ�ڵ�B��C����y���ཻ�ڵ�D��E��
��ͼ����ֱ������ϵ�У��Ե�A��3��0��ΪԲ�ģ���5Ϊ�뾶��Բ��x���ཻ�ڵ�B��C����y���ཻ�ڵ�D��E������ ��1������AD���ɴ������������D�����꣬�ҿ����C�����꣬���������߽���ʽ����������ʽ��
��2���������߽���ʽ����öԳ��ᣬ�ɵ�B��C���ڶԳ���Գƣ�����CD���Գ�����һ�㣬��õ㼴Ϊ�����P�㣬��C��D��������ֱ��CD�Ľ���ʽ��������P�����ꣻ
��3����M������꣬�ɱ�ʾ��MQ�ij�����ƽ���ı��ε����ʿ�֪BC��MQ��BC=MQ�������MQ�ij����ɵõ�����M������ķ��̣������M�����꣮
��� �⣺
��1����ͼ1������AD��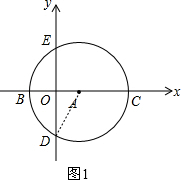
��A��3��0�����뾶Ϊ5��
��OC=OA+AC=3+5=8��
��C��8��0����
��Rt��AOD��AO=3��AD=5��
��OD=4��
��D��0��-4����
��C��D������������߽���ʽ�ɵ�$\left\{\begin{array}{l}{16+8b+c=0}\\{c=-4}\end{array}\right.$�����$\left\{\begin{array}{l}{b=-\frac{3}{2}}\\{c=-4}\end{array}\right.$��
�������߽���ʽΪy=$\frac{1}{4}$x2-$\frac{3}{2}$x-4��
��2����y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4�У���y=0�ɵ�$\frac{1}{4}$x2-$\frac{3}{2}$x-4=0�����x=-2��x=8��
���B��-2��0�����������ϣ�
��y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4=y=$\frac{1}{4}$��x-3��2-$\frac{25}{4}$��
�������߶Գ���Ϊx=3��
��B��C���ڶԳ���Գƣ�
��ͼ2������CD���Գ����ڵ�P��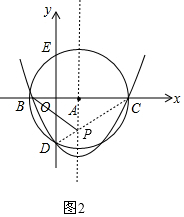
��PC=PB��
��PD+PB=PD+PC=CD��
���ʱ��PBD���ܳ���С��
��ֱ��CD�Ľ���ʽΪy=kx+s��
��$\left\{\begin{array}{l}{8k+s=0}\\{s=-4}\end{array}\right.$�����$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{s=-4}\end{array}\right.$��
��ֱ��CD����ʽΪy=$\frac{1}{2}$x-4��
��x=3ʱ���ɵ�y=-$\frac{5}{2}$��
��P��������3��-$\frac{5}{2}$����
��3����M��������x��$\frac{1}{4}$x2-$\frac{3}{2}$x-4����
���ı���BCQM��ƽ���ı��Σ�
��BC��QM��BC=QM��
��QΪ�Գ����ϵĵ㣬
��MQ=|x-3|��
��BC=8��
��|x-3|=8�����x=11��x=-5��
��x=11��x=-5ʱ��$\frac{1}{4}$x2-$\frac{3}{2}$x-4=$\frac{39}{4}$��
��������������ĵ�M��������Ϊ��11��$\frac{39}{4}$����-5��$\frac{39}{4}$����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰�������������ɶ���������ϵ��������ԳƵ����ʡ�ƽ���ı��ε����ʼ�����˼���֪ʶ���ڣ�1�������C��D�������ǽ���Ĺؼ����ڣ�2����ȷ����P���λ���ǽ���Ĺؼ����ڣ�3�������MQ�ij��ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
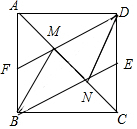 ��ͼ����������ABCD��M��N�ǶԽ���AC�ϵ����㣬��AM=CN������DM���ӳ�����AB�ڵ�F������BN���ӳ�����DC�ڵ�E������BM��DN��
��ͼ����������ABCD��M��N�ǶԽ���AC�ϵ����㣬��AM=CN������DM���ӳ�����AB�ڵ�F������BN���ӳ�����DC�ڵ�E������BM��DN���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
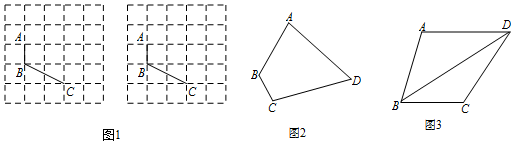
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
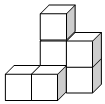 ��ͼ��ʾ�ļ�����������ͬ��С�������ɵģ��뻭����������ͼ������ͼ����ͼ��
��ͼ��ʾ�ļ�����������ͬ��С�������ɵģ��뻭����������ͼ������ͼ����ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
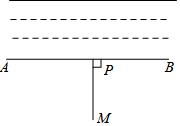 ��ͼ���ƻ��Ѻ�ˮ����ˮ��M�У�����MP��AB������ΪP��Ȼ����MP��������ʹ������������̣�������Ƶ������Ǵ��߶���̣�
��ͼ���ƻ��Ѻ�ˮ����ˮ��M�У�����MP��AB������ΪP��Ȼ����MP��������ʹ������������̣�������Ƶ������Ǵ��߶���̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
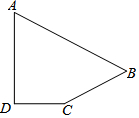 ���ı���ABCD�У���D=90�㣬AD=$\sqrt{12}$��CD=2��BC=3��AB=5�����ı���ABCD�������
���ı���ABCD�У���D=90�㣬AD=$\sqrt{12}$��CD=2��BC=3��AB=5�����ı���ABCD��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com