
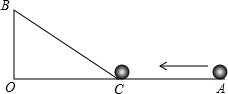
 如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少? 科目:初中数学 来源: 题型:选择题
| A. | 75° | B. | 105° | C. | 60° | D. | 45° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
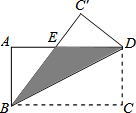 如图,长方形ABCD中,AB=16cm,BC=32cm,如果将该长方形沿对角线BD折叠,那么图中阴影部分的面积( )cm2.
如图,长方形ABCD中,AB=16cm,BC=32cm,如果将该长方形沿对角线BD折叠,那么图中阴影部分的面积( )cm2.| A. | 72 | B. | 90 | C. | 108 | D. | 160 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
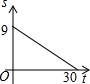 由于植被遭遇到严重破坏,某地的土地每年以相同的速度沙化,设t年后该地剩余绿地面积为S万公顷的图象如图所示,则土地沙化的速度为$\frac{3}{10}$万公顷/年,经过30年,该地的土地将全部沙化.
由于植被遭遇到严重破坏,某地的土地每年以相同的速度沙化,设t年后该地剩余绿地面积为S万公顷的图象如图所示,则土地沙化的速度为$\frac{3}{10}$万公顷/年,经过30年,该地的土地将全部沙化.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com