
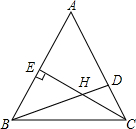
 △ABC中,∠A:∠ABC:∠ACB=3:4:5,CE是AB上的高,∠BHC=135°,求证:BD⊥AC.
△ABC中,∠A:∠ABC:∠ACB=3:4:5,CE是AB上的高,∠BHC=135°,求证:BD⊥AC. 分析 根据三角形内角和为180°,∠A:∠ABC:∠ACB=3:4:5,可以求得△ABC各内角的值,CE是AB上的高,进而求得∠BCE的值,∠HCD的值,又因为∠BHC=135°,根据外角的性质进而求得∠HDC的值,从而可证得结论成立.
解答 证明:∵在△ABC中,∠A:∠ABC:∠ACB=3:4:5,∠A+∠ABC+∠ACB=180°,
∴∠A=45°,∠ABC=60°,∠ACB=75°.
∵CE是AB上的高,
∴∠CEB=90°.
∵∠ABC=60°,∠ACB=75°,
∴∠BCE=30°,∠HCD=45°.
又∵∠BHC=135°,∠BHC=∠HCD+∠HDC,
∴∠HDC=90°.
∴BD⊥AC.
点评 本题考查三角形的内角和,垂直的性质,三角形外角的性质,关键是灵活变化,最终求出所要证明的结论.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
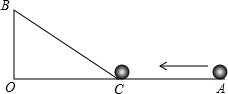 如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com