
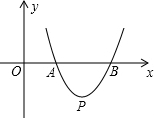
 如图,抛物线y=$\frac{\sqrt{3}}{2}{x}^{2}$-4$\sqrt{3}$x+6$\sqrt{3}$与x轴交于A、B,点P为顶点,在x轴下方的抛物线上是否存点M,使△AMP≌△AMB?若存在,求出直线AM的解析式,若不存在,试说明理由.
如图,抛物线y=$\frac{\sqrt{3}}{2}{x}^{2}$-4$\sqrt{3}$x+6$\sqrt{3}$与x轴交于A、B,点P为顶点,在x轴下方的抛物线上是否存点M,使△AMP≌△AMB?若存在,求出直线AM的解析式,若不存在,试说明理由. 分析 过点P作x轴的垂线,垂足为C,证出△APB是等边三角形,作∠PAB的平分线交抛物线于M点,连接PM,BM,由AM=AM,∠PAM=∠BAM,AB=AP得到△AMP≌△AMB,求出∠PAB的平分线与对称轴x=4的交点坐标,运用待定系数法求出直线AM的解析式.
解答 解:抛物线y=$\frac{\sqrt{3}}{2}{x}^{2}$-4$\sqrt{3}$x+6$\sqrt{3}$与x轴交于A、B,点P为顶点,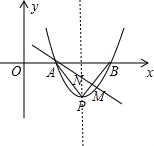
∴A(2,0),B(6,0),P(4,-2$\sqrt{3}$),
过点P作x轴的垂线,垂足为C,则PC=2$\sqrt{3}$,AC=2,
由勾股定理,可得AP=4,PB=4,又AB=4,
所以△APB是等边三角形,
只要作∠PAB的平分线交抛物线于M点,
连接PM,BM,
在△AMP和△AMB中,
$\left\{\begin{array}{l}{AM=AM}\\{∠PAM=∠BAM}\\{AB=AP}\end{array}\right.$,
∴△AMP≌△AMB.
因此即存在这样的点M,使△AMP≌△AMB.
设∠PAB的平分线与抛物线的对称轴x=4交于一点N,
点N的坐标为(4,-$\frac{2\sqrt{3}}{3}$),
设直线AM的解析式为y=kx+b,则
$\left\{\begin{array}{l}{2k+b=0}\\{4k+b=-\frac{2\sqrt{3}}{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=\frac{2\sqrt{3}}{3}}\end{array}\right.$,
∴直线AM的解析式为y=-$\frac{\sqrt{3}}{3}$x+$\frac{2\sqrt{3}}{3}$.
点评 本题主要考查了抛物线与x的交点以及数形结合思想和待定系数法求解析式,发现∠PAB的平分线交抛物线于M点,使得△AMP≌△AMB是解决本题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
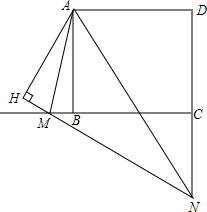 已知:如图,在正方形ABCD中,M在CB延长线上,N在DC延长线上,∠MAN=45°,AH⊥MN,垂足为H,求证:
已知:如图,在正方形ABCD中,M在CB延长线上,N在DC延长线上,∠MAN=45°,AH⊥MN,垂足为H,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
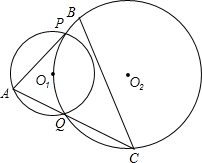 如图,⊙O1与⊙O2交于P、Q两点,且⊙O2经过点O1,A是⊙O1的优弧$\widehat{PQ}$上任一点,AP、AQ的延长线与⊙O2分别交于点B、C.证明:O1为△ABC的垂心.
如图,⊙O1与⊙O2交于P、Q两点,且⊙O2经过点O1,A是⊙O1的优弧$\widehat{PQ}$上任一点,AP、AQ的延长线与⊙O2分别交于点B、C.证明:O1为△ABC的垂心.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
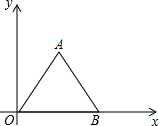 在平面直角坐标中.等边△OAB的OB在x轴上,0B=b,满足${a}^{2}-10a+25+\sqrt{b-4}=0$,D(a,0)
在平面直角坐标中.等边△OAB的OB在x轴上,0B=b,满足${a}^{2}-10a+25+\sqrt{b-4}=0$,D(a,0)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com