
【题目】如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,
(1)求∠DAB的度数,并写出理由.
(2)求∠EAC的度数.
(3)计算∠BAC的度数.
(4)根据以上条件及结论,你还能得出其他结论吗?试写出一个.
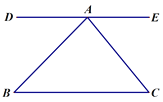
【答案】(1)∠DAB的度数为45°,根据两直线平行,内错角相等得出.(2)∠EAC的度数是50°.(3)∠BAC=180°-∠DAB-∠EAC=180°-45°-50°=95°.(4)三角形ABC的内角和是180°
【解析】(1)由平行线的性质可得到∠DAB=∠B;(2)由平行线的性质可得到∠EAC=∠C;(3)由平角的定义可求得∠BAC,(4)结合(1)(2)(3)可得出结论.
解:(1)∵DE∥BC,
∴∠DAB=∠B=45°;
(2)∵DE∥BC,
∴∠EAC=∠C=50°,
(3)∵直线DE过点A,
∴∠DAE=180°,
∴∠DAB+∠EAC+∠BAC=180°,
∴∠BAC=180°-45°-50°=85°;
(4)∵DE∥BC,
∴∠B=∠DAB,∠C=∠EAC,
∵∠DAB+∠EAC+∠BAC=180°,
∴∠B+∠C+∠BAC=180°,
即三角形内角和为180°.
“点睛”本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,④a∥b,b∥c,a∥c.


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() 在直线
在直线![]() 上,点
上,点![]() 、
、![]() 的坐标分别是(-1,0),(1,2),点
的坐标分别是(-1,0),(1,2),点![]() 的横坐标为2,过点
的横坐标为2,过点![]() 作
作![]() 轴于
轴于![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)若![]() ,
, ![]() ,求
,求![]() (用
(用![]() ,
, ![]() 表示);
表示);
(2)已知直线![]() 上的点的横坐标
上的点的横坐标![]() 与纵坐标
与纵坐标![]() 都是二元一次方程
都是二元一次方程![]() 的解(同学们可以用点
的解(同学们可以用点![]() 、
、![]() 的坐标进行检验),直线
的坐标进行检验),直线![]() 上的点的横坐标
上的点的横坐标![]() 与纵坐标
与纵坐标![]() 都是二元一次方程
都是二元一次方程![]() 的解,求点
的解,求点![]() 、
、![]() 的坐标;
的坐标;
(3)解方程组![]() ,比较该方程组的解与两条直线的交点
,比较该方程组的解与两条直线的交点![]() 的坐标,你得出什么结论?
的坐标,你得出什么结论?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强青少年的防毒拒毒意识,学校举办了一次“禁毒教育”演讲比赛,其中某位选手的演讲内容、语言表达、演讲技巧这三项得分分别为90分,80分,85分,若依次按50%,30%,20%的比例确定成绩,则该选手的最后得分是__________分.
查看答案和解析>>
科目:初中数学 来源: 题型:
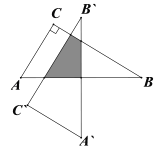
【题目】如图,在Rt△ABC中,已知∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知□ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
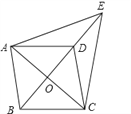
(1)四边形ABCD是菱形吗?请说明理由;
(2)若∠AED=2∠EAD,试说明四边形ABCD是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com