
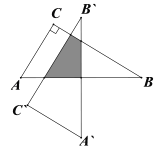
【题目】如图,在Rt△ABC中,已知∠C=90°,∠A=60°,AC=3cm,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′,则旋转前后两个直角三角形重叠部分的面积为______.
【答案】![]()
【解析】根据已知及勾股定理求得DP的长,再根据全等三角形的判定得到△B′PH≌△BPD,从而根据直角三角形的性质求得GH,BG的长,从而不难求得旋转前后两个直角三角形重叠部分的面积.
解:如图所示,
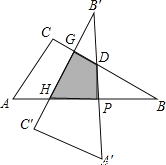
在直角△DPB中,BP=AP=AC=3,
∵∠A=60°,
∴DP2+BP2=BD2,
∴x2+32=(2x)2,
∴DP=x=![]() ,
,
∵B′P=BP,∠B=∠B′,∠B′PH=∠BPD=90°,
∴△B′PH≌△BPD,
∴PH=PD=![]() ,
,
∵在直角△BGH中,BH=3+![]() ,
,
∴GH=![]() ,BG=
,BG=![]() ,
,
∴S△BGH=![]() ×
×![]() ×
×![]() =
=![]() ,S△BDP=
,S△BDP=![]() ×3×
×3×![]() =
=![]() ,
,
∴SDGHP=![]() =
=![]() cm2.
cm2.
“点睛”此题考查勾股定理,三角形的全等的判定及性质,旋转的性质等知识的综合运用.


科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
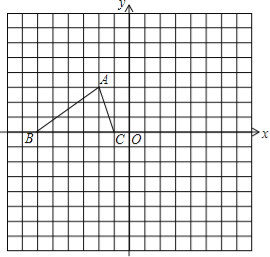
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八月份利川市政府计划在总费用2300元的限额内,租用汽车送234名运动员和6名教练到恩施州参加第二届全州青少年运动会,每辆汽车上至少要有1名教练.现有甲、乙两种大客车,它们的载客量和租金如下表:

(1)共需租多少辆汽车?
(2)有几种租车方案?
(3)最节省费用的是哪种租车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
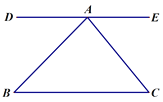
【题目】如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,
(1)求∠DAB的度数,并写出理由.
(2)求∠EAC的度数.
(3)计算∠BAC的度数.
(4)根据以上条件及结论,你还能得出其他结论吗?试写出一个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课前预习是学习数学的重要环节,为了了解所教班级学生完成数学课前预习的具体情况,王老师对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)王老师一共调查了多少名同学?
(2)C类女生有 名,D类男生有 名,将上面条形统计图补充完整;
(3)为了共同进步,王老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意掷一枚骰子,下列情况出现的可能性比较大的是( )
A. 面朝上的点数是6 B. 面朝上的点数是偶数
C. 面朝上的点数大于2 D. 面朝上的点数小于2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=(2m–2)x+m+1 (1)、m为何值时,图象过原点.(2)、已知y随x增大而增大,求m的取值范围.(3)、函数图象与y轴交点在x轴上方,求m取值范围.(4)、图象过二、一、四象限,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com