
【题目】赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:
(1)起点A与终点B之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)分别求甲、乙两支龙舟队的y与x函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?

【答案】(1)3000;(2)甲龙舟队先出发,乙龙舟队先到达终点;(3)甲:y=120x(0≤x≤25);乙:y=200x﹣1000(5≤x≤20);(4)甲龙舟队出发![]() 或10或15或
或10或15或![]() 分钟时,两支龙舟队相距200米.
分钟时,两支龙舟队相距200米.
【解析】试题分析:(1)根据函数图象即可得出起点A与终点B之间的距离;
(2)根据函数图象即可得出甲龙舟队先出发,乙龙舟队先到达终点;
(3)设甲龙舟队的y与x函数关系式为y=kx,把(25,3000)代入,可得甲龙舟队的y与x函数关系式;设乙龙舟队的y与x函数关系式为y=ax+b,把(5,0),(20,3000)代入,可得乙龙舟队的y与x函数关系式;
(4)分四种情况进行讨论,根据两支龙舟队相距200米分别列方程求解即可.
试题解析:解:(1)由图可得,起点A与终点B之间相距3000米;
(2)由图可得,甲龙舟队先出发,乙龙舟队先到达终点;
(3)设甲龙舟队的y与x函数关系式为y=kx,把(25,3000)代入,可得3000=25k,解得k=120,∴甲龙舟队的y与x函数关系式为y=120x(0≤x≤25),设乙龙舟队的y与x函数关系式为y=ax+b,把(5,0),(20,3000)代入,可得: ![]() ,解得:
,解得: ![]() ,∴乙龙舟队的y与x函数关系式为y=200x﹣1000(5≤x≤20);
,∴乙龙舟队的y与x函数关系式为y=200x﹣1000(5≤x≤20);
(4)令120x=200x﹣1000,可得x=12.5,即当x=12.5时,两龙舟队相遇,当x<5时,令120x=200,则x=![]() (符合题意);
(符合题意);
当5≤x<12.5时,令120x﹣(200x﹣1000)=200,则x=10(符合题意);
当12.5<x≤20时,令200x﹣1000﹣120x=200,则x=15(符合题意);
当20<x≤25时,令3000﹣120x=200,则x=![]() (符合题意);
(符合题意);
综上所述,甲龙舟队出发![]() 或10或15或
或10或15或![]() 分钟时,两支龙舟队相距200米.
分钟时,两支龙舟队相距200米.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】随着私家车拥有量的增加,停车问题已经给人们的生活带来了很多不便.为了缓解停车矛盾,某小区开发商欲投资16万元,建造若干个停车位,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的3倍.据测算,建造费用及年租金如下表:
类别 | 室内车位 | 露天车位 |
建造费用(元/个) | 5 000 | 1 000 |
年租金(元/个) | 2 000 | 800 |
(1)该开发商有哪几种符合题意的建造方案?写出解答过程.
(2)若按表中的价格将两种车位全部出租,哪种方案获得的年租金最多?并求出此种方案的年租金.(不考虑其他费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有如下一串二次根式:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() …
…
(1)求①,②,③,④的值;
(2)仿照①,②,③,④,写出第⑤个二次根式;
(3)仿照①,②,③,④,⑤,写出第n个二次根式,并化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一个含30°的直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(图中∠OMN=30°,∠NOM=90°)
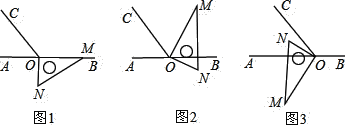
(1)将图1中的三角板绕点O逆时针旋转至图2,使OM在∠BOC的内部,且恰好平分∠BOC,问直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t;
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购买60件A商品和30件B商品共用了1080元,购买50件A商品和20件B商品共用了880元.
(1)A、B两种商品的单价分别是多少元?
(2)已知该商店购买B商品的件数比购买A商品的件数的2倍少4件,如果需要购买A、B两种商品的总件数不少于32件,且该商店购买的A、B两种商品的总费用不超过296元,那么该商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )

A. 25° B. 30° C. 35° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现与探索.
(1)根据小明的解答(图1)将下列各式因式分解

①a2-12a+20
②(a-1)2-8(a-1)+7
③a2-6ab+5b2
(2)根据小丽的思考(图2)解决下列问题.
①说明:代数式a2-12a+20的最小值为-16.
②请仿照小丽的思考解释代数式-(a+1)2+8的最大值为8,并求代数式-a2+12a-8的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com