
【题目】发现与探索.
(1)根据小明的解答(图1)将下列各式因式分解

①a2-12a+20
②(a-1)2-8(a-1)+7
③a2-6ab+5b2
(2)根据小丽的思考(图2)解决下列问题.
①说明:代数式a2-12a+20的最小值为-16.
②请仿照小丽的思考解释代数式-(a+1)2+8的最大值为8,并求代数式-a2+12a-8的最大值.
【答案】(1) ①(a-10)(a-2); ②(a-7)(a-3); ③(a-5b)(a-b);(2) ①见解析;②-a2+12a-8的最大值为28
【解析】
参照例题可得相应解法
(1)根据小明的解答将下列各式因式分解
①a2-12a+20
解原式=a2-12a+36-36+20
=(a-6)2-42
=(a-10)(a-2)
②(a-1)2-8(a-1)+12
解原式=(a-1)2-8(a-1)+16-16+12
=(a-5)2-22
=(a-7)(a-3)
③a2-6ab+5b2
解原式=a2-6ab+9b2-9b2+5b2
=(a-3b)2-4b2
=(a-5b)(a-b)
(2)①说明:代数式a2-12a+20的最小值为-16.
a2-12a+20
解原式=a2-12a+36-36+20
=(a-6)2-16
∵无论a取何值(a-6)2都≥0
∴代数式(a-6)2-16≥-16,
∴a2-12a+20的最小值为-16.
②∵无论a取何值-(a+1)2≤0
∴代数式-(a+1)2+8小于等于8,
则-(a+1)2+8的最大值为8.
-a2+12a-8.
解原式=-(a2-12a+8)
=-(a2-12a+36-36+8)
=-(a-6)2+36-8
=-(a-6)2+28
∵a取何值-(a-6)2≤0,
∴代数式-(a-6)2+28≤28
∴-a2+12a-8的最大值为28.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:
(1)起点A与终点B之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)分别求甲、乙两支龙舟队的y与x函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作探究:已知在纸面上有一数轴(如图所示).
![]()
操作一:
(1)折叠纸面,使1表示的点与-1表示的点重合,则-3表示的点与________表示的点重合;
操作二:
(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数________表示的点重合;
②若数轴上A、B两点之间距离为11(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)求证:2CD2=AD2+DB2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣2ax+c(a<0)的最大值为4,且抛物线过点( ![]() ,﹣
,﹣ ![]() ),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
(1)求该二次函数的解析式,及顶点D的坐标;
(2)求|PC﹣PD|的最大值及对应的点P的坐标;
(3)设Q(0,2t)是y轴上的动点,若线段PQ与函数y=a|x|2﹣2a|x|+c的图象只有一个公共点,求t的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
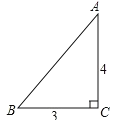
【题目】如图,一张三角形纸片ABC,其中![]() ,
,![]() ,
,![]() 现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处
现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处![]() 这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是
这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2 , 则它移动的距离AA′等于( ) 
A.0.5cm
B.1cm
C.1.5cm
D.2cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com