
【题目】已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)求证:2CD2=AD2+DB2 .
【答案】
(1)
证明:∵△ABC和△ECD都是等腰直角三角形,
∴AC=BC,CD=CE,
∵∠ACB=∠DCE=90°,
∴∠ACE+∠ACD=∠BCD+∠ACD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
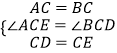 ,
,
∴△AEC≌△BDC(SAS)
(2)
证明:∵△ACB是等腰直角三角形,
∴∠B=∠BAC=45度.
∵△ACE≌△BCD,
∴∠B=∠CAE=45°
∴∠DAE=∠CAE+∠BAC=45°+45°=90°,
∴AD2+AE2=DE2.
由(1)知AE=DB,
∴AD2+DB2=DE2,即2CD2=AD2+DB2
【解析】(1)本题要判定△ACE≌△BCD,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,则DC=EA,AC=BC,∠ACB=∠ECD,又因为两角有一个公共的角∠ACD,所以∠BCD=∠ACE,根据SAS得出△ACE≌△BCD;
(2)由(1)的论证结果得出∠DAE=90°,AE=DB,从而求出AD2+DB2=DE2 , 即2CD2=AD2+DB2 . 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,以及等角的余角相等的性质,熟记各性质是解题的关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】有如下一串二次根式:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() …
…
(1)求①,②,③,④的值;
(2)仿照①,②,③,④,写出第⑤个二次根式;
(3)仿照①,②,③,④,⑤,写出第n个二次根式,并化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )

A. 25° B. 30° C. 35° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
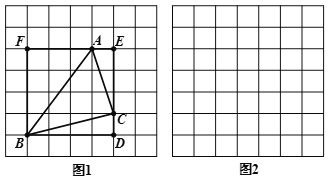
【题目】莫小贝在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC 的面积.
(1)莫小贝所画的△ABC 的三边长分别是AB=_______,BC=______,AC=______;△ABC 的面积为________.
(2)已知△ABC 中,AB=![]() ,BC=
,BC=![]() ,AC=
,AC=![]() ,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
,请你根据莫小贝的思路,在图2中画出△ABC ,并直接写出△ABC的面积_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
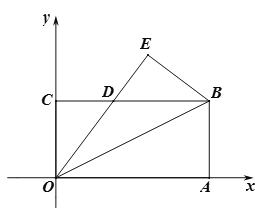
【题目】如图,矩形OABC的边OA,OC分别与坐标轴重合,并且点B的坐标为![]() .将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
.将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
(1)求证:△OBD为等腰三角形;
(2)求点E的坐标;
(3)坐标平面内是否存在一点F,使得以点B,E,F,O为顶点的四边形是平行四边形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现与探索.
(1)根据小明的解答(图1)将下列各式因式分解

①a2-12a+20
②(a-1)2-8(a-1)+7
③a2-6ab+5b2
(2)根据小丽的思考(图2)解决下列问题.
①说明:代数式a2-12a+20的最小值为-16.
②请仿照小丽的思考解释代数式-(a+1)2+8的最大值为8,并求代数式-a2+12a-8的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y= ![]() (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0). 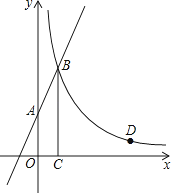
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y= ![]() (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com