
【题目】已知二次函数y=ax2﹣2ax+c(a<0)的最大值为4,且抛物线过点( ![]() ,﹣
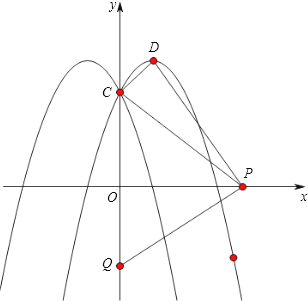
,﹣ ![]() ),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
),点P(t,0)是x轴上的动点,抛物线与y轴交点为C,顶点为D.
(1)求该二次函数的解析式,及顶点D的坐标;
(2)求|PC﹣PD|的最大值及对应的点P的坐标;
(3)设Q(0,2t)是y轴上的动点,若线段PQ与函数y=a|x|2﹣2a|x|+c的图象只有一个公共点,求t的取值.
【答案】
(1)
解:∵y=ax2﹣2ax+c的对称轴为:x=﹣ ![]() =1,
=1,
∴抛物线过(1,4)和( ![]() ,﹣
,﹣ ![]() )两点,
)两点,
代入解析式得: 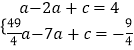 ,
,
解得:a=﹣1,c=3,
∴二次函数的解析式为:y=﹣x2+2x+3,
∴顶点D的坐标为(1,4);
(2)
解:∵C、D两点的坐标为(0,3)、(1,4);
由三角形两边之差小于第三边可知:
|PC﹣PD|≤|CD|,
∴P、C、D三点共线时|PC﹣PD|取得最大值,此时最大值为,
|CD|= ![]() ,
,
由于CD所在的直线解析式为y=x+3,
将P(t,0)代入得t=﹣3,
∴此时对应的点P为(﹣3,0)
(3)
解:y=a|x|2﹣2a|x|+c的解析式可化为:
y= ![]()
设线段PQ所在的直线解析式为y=kx+b,将P(t,0),Q(0,2t)代入得:
线段PQ所在的直线解析式:y=﹣2x+2t,
∴①当线段PQ过点(0,3),即点Q与点C重合时,线段PQ与函数
y= ![]() 有一个公共点,此时t=
有一个公共点,此时t= ![]() ,
,
当线段PQ过点(3,0),即点P与点(3,0)重合时,t=3,此时线段PQ与
y= ![]() 有两个公共点,所以当
有两个公共点,所以当 ![]() ≤t<3时,
≤t<3时,
线段PQ与y= ![]() 有一个公共点,
有一个公共点,
②将y=﹣2x+2t代入y=﹣x2+2x+3(x≥0)得:
﹣x2+2x+3=﹣2x+2t,
﹣x2+4x+3﹣2t=0,
令△=16﹣4(﹣1)(3﹣2t)=0,
t= ![]() >0,
>0,
所以当t= ![]() 时,线段PQ与y=
时,线段PQ与y= ![]() 也有一个公共点,
也有一个公共点,
③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ只与
y=﹣x2﹣2x+3(x<0)有一个公共点,此时t=﹣3,
所以当t≤﹣3时,线段PQ与y= ![]() 也有一个公共点,
也有一个公共点,
综上所述,t的取值是 ![]() ≤t<3或t=
≤t<3或t= ![]() 或t≤﹣3.
或t≤﹣3.
【解析】(1)先利用对称轴公式x=﹣ ![]() 计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;
计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;
(2)根据三角形的三边关系:可知P、C、D三点共线时|PC﹣PD|取得最大值,求出直线CD与x轴的交点坐标,就是此时点P的坐标;
(3)先把函数中的绝对值化去,可知y= 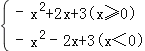 ,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ过点(0,3),即点Q与点C重合时,两图象有一个公共点,当线段PQ过点(3,0),即点P与点(3,0)重合时,两函数有两个公共点,写出t的取值;②线段PQ与当函数y=a|x|2﹣2a|x|+c(x≥0)时有一个公共点时,求t的值;③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ与当函数y=a|x|2﹣2a|x|+c(x<0)时也有一个公共点,则当t≤﹣3时,都满足条件;综合以上结论,得出t的取值.本题考查了二次函数的综合应用,先利用待定系数法求解析式,同时把最大值与三角形的三边关系联系在一起;同时对于二次函数利用动点求取值问题,从特殊点入手,把函数分成几部分考虑,按自变量从大到小的顺序或从小到大的顺序求解.
,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ过点(0,3),即点Q与点C重合时,两图象有一个公共点,当线段PQ过点(3,0),即点P与点(3,0)重合时,两函数有两个公共点,写出t的取值;②线段PQ与当函数y=a|x|2﹣2a|x|+c(x≥0)时有一个公共点时,求t的值;③当线段PQ过点(﹣3,0),即点P与点(﹣3,0)重合时,线段PQ与当函数y=a|x|2﹣2a|x|+c(x<0)时也有一个公共点,则当t≤﹣3时,都满足条件;综合以上结论,得出t的取值.本题考查了二次函数的综合应用,先利用待定系数法求解析式,同时把最大值与三角形的三边关系联系在一起;同时对于二次函数利用动点求取值问题,从特殊点入手,把函数分成几部分考虑,按自变量从大到小的顺序或从小到大的顺序求解.


科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将一个含30°的直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(图中∠OMN=30°,∠NOM=90°)
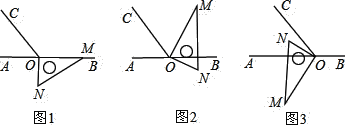
(1)将图1中的三角板绕点O逆时针旋转至图2,使OM在∠BOC的内部,且恰好平分∠BOC,问直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t;
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在东西方向的海岸线MN上有A,B两港口,海上有一座小岛P,渔民每天都乘轮船从A,B 两港口沿AP,BP的路线去小岛捕鱼作业.已知小岛P在A港的北偏东60°方向,在B港的北偏西45°方向,小岛P距海岸线MN的距离为30海里.
(1)求AP,BP的长(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7,
≈1.7,![]() ≈2.2);
≈2.2);
(2)甲、乙两船分别从A,B两港口同时出发去小岛P捕鱼作业,甲船比乙船晚到小岛24分钟.已知甲船速度是乙船速度的1.2倍,利用(1)中的结果求甲、乙两船的速度各是多少海里/时?

查看答案和解析>>
科目:初中数学 来源: 题型:
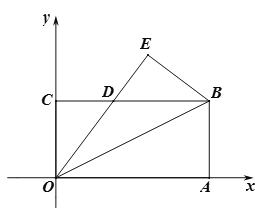
【题目】如图,矩形OABC的边OA,OC分别与坐标轴重合,并且点B的坐标为![]() .将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
.将该矩形沿OB折叠,使得点A落在点E处,OE与BC的交点为D.
(1)求证:△OBD为等腰三角形;
(2)求点E的坐标;
(3)坐标平面内是否存在一点F,使得以点B,E,F,O为顶点的四边形是平行四边形,若存在,请直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现与探索.
(1)根据小明的解答(图1)将下列各式因式分解

①a2-12a+20
②(a-1)2-8(a-1)+7
③a2-6ab+5b2
(2)根据小丽的思考(图2)解决下列问题.
①说明:代数式a2-12a+20的最小值为-16.
②请仿照小丽的思考解释代数式-(a+1)2+8的最大值为8,并求代数式-a2+12a-8的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
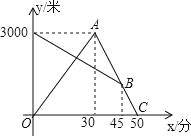
【题目】某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
(1)求张强返回时的速度;
(2)妈妈比按原速返回提前多少分钟到家?
(3)请直接写出张强与妈妈何时相距1000米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两点在数轴上如图所示,其中O为原点,点A对应的有理数为a,点B对应的有理数为b,且点A距离原点6个单位长度,a.b满足b-|a|=2.
(1)a=______;b=______;
(2)动点P从点A出发,以每秒2个单位长度的速度向右运动,设运动时间为t秒(t>0)
①当PO=2PB时,求点P的运动时间t:
②当PB=6时,求t的值:
(3)当点P运动到线段OB上时,分别取AP和OB的中点E、F,则![]() 的值是否为一个定值?如果是,求出定值,如果不是,说明理由.
的值是否为一个定值?如果是,求出定值,如果不是,说明理由.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com