
����Ŀ��ij���糿����ǿ�Ӽ��ܲ�ȥ����������ͬʱ��������������������ؼң�;��������������ǿ�ܵ�����������Ҫ���꣬������ԭ·���أ��������������һ��ص��ң���ǿ������ʼ����ͬһ����ֱ�Ĺ�·�����ߣ�����ͼ��������ҵľ���y���ף�����ǿ������ʱ��x���֣�֮��ĺ���ͼ����ͼ����Ϣ����������⣺
��1������ǿ����ʱ���ٶȣ�
��2������Ȱ�ԭ�ٷ�����ǰ���ٷ��ӵ��ң�
��3����ֱ��д����ǿ�������ʱ���1000�ף�
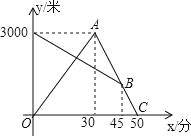
���𰸡�(1)��150��/�֣�(2)��10�֣�(3)��35�ֻ�![]() �ֻ�
�ֻ�![]() ��
��
��������
���������(1)�������ٶ�=·����ʱ�䣬���ɽ��(2)���������ԭ�����ٶȣ�����ԭ������3000�����õ�ʱ�䣬���ɽ��(3)���ֱ������ǿ������ĺ�������ʽ��������ǿ���������1000�ף��г����̣����ɽ��
���������(1)��3000����50��30��=3000��20=150����/�֣���
����ǿ����ʱ���ٶ�Ϊ150��/�֣�
(2)����45��30����150=2250���ף�����B������Ϊ��45��750����
����ԭ�����ٶ�Ϊ��2250��45=50����/�֣��� ����ԭ���ؼ����õ�ʱ��Ϊ��3000��50=60���֣���
60��50=10���֣��� ����Ȱ�ԭ�ٷ�����ǰ10���ӵ��ң�
(3)����ͼ��
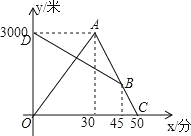
���߶�BD�ĺ�������ʽΪ��y=kx+b��
�ѣ�0��3000������45��750������ã�![]() ����ã�
����ã�![]() �� ��y=��50x+3000��
�� ��y=��50x+3000��
�߶�OA�ĺ�������ʽΪ��y=100x��0��x��30���� ���߶�AC�Ľ���ʽΪ��y=k1x+b1��
�ѣ�30��3000������50��0������ã�![]() ��ã�
��ã�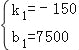 ��
��
��y=��150x+7500����30��x��50��
����ǿ���������1000��ʱ��
����50x+3000��100x=1000��100x������50x+3000��=1000����150x+7500��������50x+3000��=1000��
��ã�x=35��x=![]() ��x=
��x=![]() �� ����ʱ��Ϊ35�ֻ�
�� ����ʱ��Ϊ35�ֻ�![]() �ֻ�
�ֻ�![]() ��ʱ����ǿ�������ʱ���1000�ף�
��ʱ����ǿ�������ʱ���1000�ף�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬��ACΪһ���������ȱ�������ACD����EΪAB���е㣬����DE�� 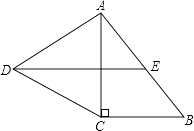
��1��֤��DE��CB��
��2��̽��AC��AB����������������ϵʱ���ı���DCBE��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ, ��֪��1����2��180o, ��3����B, ��˵����DEC����C��180o. �����������գ�
�⣺�ߡ�1����2��180o����֪��

�֡ߡ�1�� ��180o��ƽ�Ƕ��壩
���2�� ��ͬ�ǵIJ�����ȣ�
�� ���ڴ�����ȣ���ֱ��ƽ�У�
���3 �� ����ֱ��ƽ�У��ڴ�����ȣ�
�֡ߡ�3����B����֪��
�� ������������
�� �� �� ��
���DEC����C��180o�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a+b=-7��ab=10�������ʽ��3ab+6a+4b��-��2a-2ab����ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a=��1��b=1ʱ����a3��b3������a3��3a2b+3ab2��b3����ֵ�ǣ� ��
A.0
B.6
C.��6
D.9
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�E��F�ǶԽ���BD�ϵĵ㣬��1=��2�� 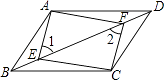
��1����֤��BE=DF��
��2����֤��AF��CE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��PΪRt��ABC����ƽ��������һ�㣨����ֱ��AC�ϣ�����ACB=90�㣬MΪAB���е㣮��������PA��PCΪ�ڱ���ƽ���ı���PADC������PM���ӳ�����E��ʹME=PM������DE�� ̽����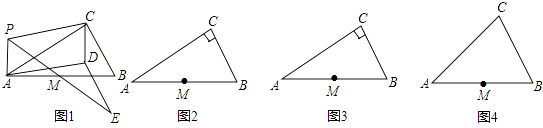
��1����������߶�DE�йص��������ۣ�
��2����������ͼ2��ͼ3ѡ��ͬλ�õĵ�P����������������
��3��������2��֮���������Ϊ��д�Ľ�������ȷ�ģ������֤���� �������Ϊ��д�Ľ����Ǵ���ģ�����ͼ2��ͼ3����˵����
��ע�⣺����Ľ��ۣ�ֻҪ���÷�������˵��Ҳ�÷֣�
��4��������Rt��ABC����Ϊ�������ABC���������������䣬����ͼ4��������д�����߶�DE�йصĽ��ۣ�ֱ��д�𰸣���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com