
【题目】如图, 已知∠1+∠2=180o, ∠3=∠B, 试说明∠DEC+∠C=180o. 请完成下列填空:
解:∵∠1+∠2=180o(已知)

又∵∠1+ =180o(平角定义)
∴∠2= (同角的补角相等)
∴ (内错角相等,两直线平行)
∴∠3 = (两直线平行,内错角相等)
又∵∠3=∠B(已知)
∴ (等量代换)
∴ ∥ ( )
∴∠DEC+∠C=180o( )
【答案】见解析
【解析】试题分析:根据同角的补角可证: ∠2=∠4,再根据内错角相等,两直线平行可证得: AB∥EF , 根据两直线平行,内错角相等可得:∠3=∠ADE,等量代换可得∠ADE=∠B ,
再利用同位角相等两直线平行可得: DE∥BC,利用两直线平行,同旁内角互补可得:∠DEC+∠C =180°.
试题解析:∵∠1+∠2=180°(已知),
又∵∠1+ ∠4 =180°(平角定义),
∴∠2= ∠4 (同角的补角相等),
∴ AB∥EF (内错角相等,两直线平行),
∴∠3= ∠ADE (两直线平行,内错角相等),
又∵∠3=∠B(已知),
∴ ∠ADE=∠B (等量代换),
DE ∥ BC ( 同位角相等,两直线平行 ),
∴∠DEC+∠C =180°( 两直线平行,同旁内角互补 ).


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
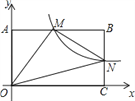
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=–![]() x+3交AB,BC于点M,N,反比例函数
x+3交AB,BC于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.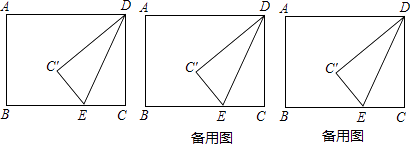
(1)若点C′刚好落在对角线BD上时,BC′=;
(2)当B C′∥DE时,求CE的长;
(3)若点C′刚好落在线段AD的垂直平分线上时,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
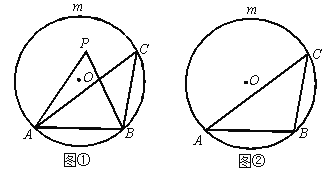
【题目】已知AB是⊙O的一条弦,点C是优弧![]() 上一点.
上一点.
(1)如图①,若点P是弦AB与![]() 所围成的弓形区域(不含弦AB与
所围成的弓形区域(不含弦AB与![]() )内一点.求证:∠APB>∠ACB;
)内一点.求证:∠APB>∠ACB;
(2)如图①,若点P在弦AB上方,且满足∠APB=∠ACB,则点P在![]() 上吗?为什么?
上吗?为什么?
(3)请在图②中直接用阴影部分表示出在弦AB与![]() 所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
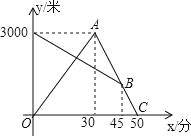
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 米,甲机器人前2分钟的速度为 米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段FG∥x轴,则此段时间,甲机器人的速度为 米/分;
(4)求A、C两点之间的距离;
(5)直接写出两机器人出发多长时间相距28米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早晨,张强从家跑步去体育锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起回到家(张强和妈妈始终在同一条笔直的公路上行走).如图是两人离家的距离y(米)与张强出发的时间x(分)之间的函数图象,根据图象信息解答下列问题:
(1)求张强返回时的速度;
(2)妈妈比按原速返回提前多少分钟到家?
(3)请直接写出张强与妈妈何时相距1000米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com