
【题目】已知AB是⊙O的一条弦,点C是优弧![]() 上一点.
上一点.
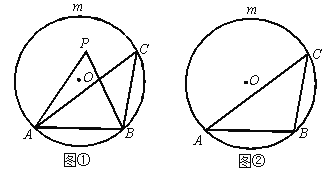
(1)如图①,若点P是弦AB与![]() 所围成的弓形区域(不含弦AB与
所围成的弓形区域(不含弦AB与![]() )内一点.求证:∠APB>∠ACB;
)内一点.求证:∠APB>∠ACB;
(2)如图①,若点P在弦AB上方,且满足∠APB=∠ACB,则点P在![]() 上吗?为什么?
上吗?为什么?
(3)请在图②中直接用阴影部分表示出在弦AB与![]() 所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
【答案】(1)证明见解析;
(2)在,理由见解析;
(3)如图见解析.
【解析】试题分析:(1)根据题意画出相应的图形,根据三角形的外角大于任何一个和它不相邻的内角,可以证明结论成立,本题得以解决;(2)点P在![]() 上,利用(1)的结论和同(1)的方法即可得出结论;(3)根据题意和第(1)问,可以画出满足∠ACB<∠APB<2∠ACB的点P所在的范围,本题得以解决
上,利用(1)的结论和同(1)的方法即可得出结论;(3)根据题意和第(1)问,可以画出满足∠ACB<∠APB<2∠ACB的点P所在的范围,本题得以解决
试题解析:(1)证明:如下图②所示,
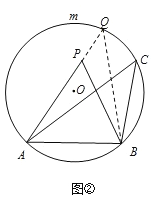
延长AP交O于点Q,连接BQ.
则∠PQB=∠ACB,
∵∠APB为△PQB的一个外角,
∴∠APB>∠PQB,
即∠APB>∠ACB;
(2)点P在![]() 上,
上,
理由:由(1)知,点P是弦AB与![]() 所围成的弓形区域(不含弦AB与
所围成的弓形区域(不含弦AB与![]() )内一点,∠APB>∠ACB,
)内一点,∠APB>∠ACB,
同(1)的方法,点P在弦AB上半部分时,利用三角形的外角,得,∠APB<∠ACB,
∴点P在![]() 上,
上,
(3)
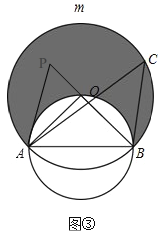
连接AO,BO,延长BO,在BO的延长线上取一点P连接AP,
∵∠AOB是△APO的外角,
∴∠AOB>∠APB,
∵∠AOB是在O中劣弧AB所对的圆心角,∠ACB是O中劣弧AB所对的圆周角,
∴∠AOB=2∠ACB,
∴点P所在的范围如下图③所示,


科目:初中数学 来源: 题型:
【题目】定义:数学活动课上,陈老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
(1)理解:
如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;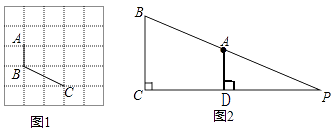
(2)应用:
如图2,在Rt△PBC中,∠PCB=90°,BC=9,点A在BP边上,且AB=13.AD⊥PC,CD=12,若PC上存在符合条件的点M,使四边形ABCM为对等四边形,求出CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
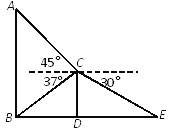
【题目】某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
(1)求建筑物CD的高度;
(2)求建筑物AB的高度.
(结果精确到0.1米,参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知∠1+∠2=180o, ∠3=∠B, 试说明∠DEC+∠C=180o. 请完成下列填空:
解:∵∠1+∠2=180o(已知)

又∵∠1+ =180o(平角定义)
∴∠2= (同角的补角相等)
∴ (内错角相等,两直线平行)
∴∠3 = (两直线平行,内错角相等)
又∵∠3=∠B(已知)
∴ (等量代换)
∴ ∥ ( )
∴∠DEC+∠C=180o( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com