
【题目】某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
(1)求建筑物CD的高度;
(2)求建筑物AB的高度.
(结果精确到0.1米,参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
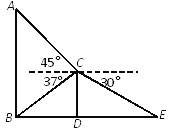
【答案】(1)CD=5.2m ;(2)AB=12.1m
【解析】试题分析:(1)由在Rt△CDE中,tan∠CED=![]() ,DE=9,∠CED=30°,即可求得答案;(2)首先过点C作CF⊥AB于点F,然后在Rt△CBF中,求得FC,在Rt△AFC中,求得AF,继而求得答案.
,DE=9,∠CED=30°,即可求得答案;(2)首先过点C作CF⊥AB于点F,然后在Rt△CBF中,求得FC,在Rt△AFC中,求得AF,继而求得答案.
试题解析:(1)在Rt△CDE中,tan∠CED=![]() ,DE=9,∠CED=30°,
,DE=9,∠CED=30°,
∴tan30°=![]() ,
,
解得:DC≈![]() ≈5.2,
≈5.2,
∴建筑物CD的高度约为5.2米;
(2)过点C作CF⊥AB于点F.
在Rt△CBF中,tan∠FCB=![]() ,BF=DC=5.2,∠FCB=37°,
,BF=DC=5.2,∠FCB=37°,
∴tan37°=![]() ≈
≈![]() ,FC≈6.93,
,FC≈6.93,
在Rt△AFC中,∵∠ACF=45°,
∴AF=CF=6.93,
∴AB=AF+BF≈12.1,
∴建筑物AB的高度约为12.1米。


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,正方形OABC的顶点O与原点重合,顶点A.C分别在x轴、y轴上,反比例函数![]() 的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
的图象与正方形的两边AB、BC分别交于点M、N,ND⊥x轴,垂足为D,连接OM、ON、MN.下列结论:
①△OCN≌△OAM;
②ON=MN;
③四边形DAMN与△MON面积相等;
④若∠MON=450,MN=2,则点C的坐标为![]() .
.
其中正确的个数是( )
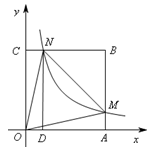
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
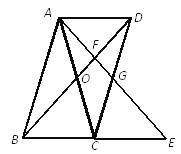
【题目】如图,□ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.
(1) 求证:△ADB≌△CEA;
(2) 若BD=6,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(m1,n1),B(m2,n2)(m1<m2)在一次函数y=kx+b的图像上.
(1)若n1-n2 +![]() (m1-m2)=0,求k的值;
(m1-m2)=0,求k的值;
(2)若m1+m2=3b,n1+n2=kb+4,b>2.试比较n1和n2的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
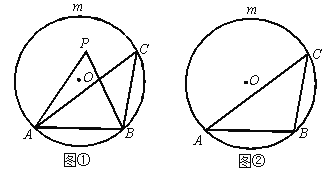
【题目】已知AB是⊙O的一条弦,点C是优弧![]() 上一点.
上一点.
(1)如图①,若点P是弦AB与![]() 所围成的弓形区域(不含弦AB与
所围成的弓形区域(不含弦AB与![]() )内一点.求证:∠APB>∠ACB;
)内一点.求证:∠APB>∠ACB;
(2)如图①,若点P在弦AB上方,且满足∠APB=∠ACB,则点P在![]() 上吗?为什么?
上吗?为什么?
(3)请在图②中直接用阴影部分表示出在弦AB与![]() 所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com