
【题目】已知点A(m1,n1),B(m2,n2)(m1<m2)在一次函数y=kx+b的图像上.
(1)若n1-n2 +![]() (m1-m2)=0,求k的值;
(m1-m2)=0,求k的值;
(2)若m1+m2=3b,n1+n2=kb+4,b>2.试比较n1和n2的大小,并说明理由.
【答案】(1)![]() (2)
(2)![]() ,理由见解析.
,理由见解析.
【解析】试题分析:(1)由一次函数图象上点的坐标特征即可得出n1=km1+b、n2=km2+b,二者做差即可得出n1-n2=k(m1-m2),再根据n1-n2+![]() (m1-m2)=0结合m1<m2即可求出k值;(2)由m1+m2=3b、n1+n2=kb+4,即可得出3kb+2b=kb+4,用函数b的代数式表示出k值,根据b的取值范围即可得出k<0,结合一次函数的性质即可得出一次函数y=kx+b中y随x的增大而减小,再根据m1<m2即可得出n1>n2.
(m1-m2)=0结合m1<m2即可求出k值;(2)由m1+m2=3b、n1+n2=kb+4,即可得出3kb+2b=kb+4,用函数b的代数式表示出k值,根据b的取值范围即可得出k<0,结合一次函数的性质即可得出一次函数y=kx+b中y随x的增大而减小,再根据m1<m2即可得出n1>n2.
试题解析:(1)∵点A(m1,n1),B(m2,n2)(m1<m2)在一次函数y=kx+b的图象上,
∴n1=km1+b、n2=km2+b,
∴n1n2=(km1+b)(km2+b)=k(m1m2),
∵n1n2+![]() (m1m2)=0,
(m1m2)=0,
∴k(m1m2)+![]() (m1m2)=0,
(m1m2)=0,
∴(k+![]() )(m1m2)=0,
)(m1m2)=0,
∵m1<m2,
∴k=![]() ;
;
(2)n1>n2,理由如下:
∵n1+n2=(km1+b)+(km2+b)=k(m1+m2)+2b=kb+4,,m1+m2=3b,
∴3kb+2b=kb+4,
解得:k=![]() .
.
∵b>2.
∴k=![]() <0,
<0,
∴一次函数y=kx+b中y随x的增大而减小。
又∵m1<m2,
∴n1>n2.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】下列两个变量成反比例函数关系的是( )
①三角形底边为定值,它的面积S和这条边上的高线h;
②三角形的面积为定值,它的底边a与这条边上的高线h;
③面积为定值的矩形的长与宽;
④圆的周长与它的半径.
A.①④B.①③C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
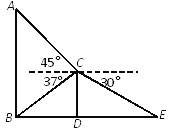
【题目】某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
(1)求建筑物CD的高度;
(2)求建筑物AB的高度.
(结果精确到0.1米,参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
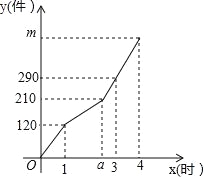
【题目】某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
(1)甲车间每小时生产产品 件,a= .
(2)求乙车间更换新设备之后y与x之间的函数关系式,并求m的值.
(3)若乙车间在开始更换新设备时,增加两名工作人员,这样可便更换设备时间减少0.5小时,并且更换后工作效率提高到原来的2倍,那么两个车间完成原任务量需几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某城区四校决定联合购买一批足球运动装备.市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少元;
(2)若城区四校联合购买100套队服和a(a>10)个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花发费用;
(3)在(2)的条件下,若a=60,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com