
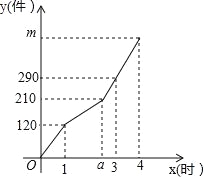
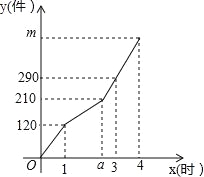
【题目】某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
(1)甲车间每小时生产产品 件,a= .
(2)求乙车间更换新设备之后y与x之间的函数关系式,并求m的值.
(3)若乙车间在开始更换新设备时,增加两名工作人员,这样可便更换设备时间减少0.5小时,并且更换后工作效率提高到原来的2倍,那么两个车间完成原任务量需几小时?
【答案】(1)60,![]() 小时;
小时;
(2)乙车间更换新设备之后y与x之间的函数关系式为:y=160x﹣190,
∴m=450件;
(3)两个车间完成原任务量需要的时间是![]() 小时.
小时.
【解析】
试题分析:(1)由开始甲、乙两个车间工作效率相同,于是得到开始甲、乙两个车间工作效率是每小时生产产品60个,即可得到结论;
(2)设乙车间更换新设备之后y与x之间的函数关系式为:y=kx+b,把(![]() ,210),(3,290)代入y=kx+b列方程组即可得到结论;
,210),(3,290)代入y=kx+b列方程组即可得到结论;
(3)根据两个车间完成原任务量需要的时间=乙车间更换新设备前的时间+乙车间更换新设备中的时间+乙车间更换新设备后的时间,即可得到结论.
试题解析:(1)∵开始甲、乙两个车间工作效率相同,
∴开始甲、乙两个车间工作效率是每小时生产产品60个,
∴a=![]() +1=
+1=![]() 小时,
小时,
故答案为:60,![]() 小时;
小时;
(2)设乙车间更换新设备之后y与x之间的函数关系式为:y=kx+b,
把(![]() ,210),(3,290)代入y=kx+b得:
,210),(3,290)代入y=kx+b得: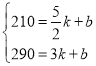 ,
,
∴![]() ,
,
∴乙车间更换新设备之后y与x之间的函数关系式为:y=160x﹣190,
当x=4时,y=450,
∴m=450件;
(3)两个车间完成原任务量需要的时间=乙车间更换新设备前的时间+乙车间更换新设备中的时间+乙车间更换新设备后的时间,
即1+(![]() ﹣1﹣
﹣1﹣![]() )﹣
)﹣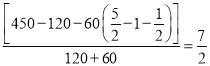
答:两个车间完成原任务量需要的时间是![]() 小时.
小时.


科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(m1,n1),B(m2,n2)(m1<m2)在一次函数y=kx+b的图像上.
(1)若n1-n2 +![]() (m1-m2)=0,求k的值;
(m1-m2)=0,求k的值;
(2)若m1+m2=3b,n1+n2=kb+4,b>2.试比较n1和n2的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F是ABCD对角线AC上两点,AE=CF. 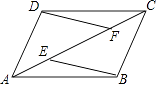
(1)求证:△ABE≌△CDF;
(2)连结DE,BF,求证:四边形DEBF是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com