
【题目】如图,E、F是ABCD对角线AC上两点,AE=CF. 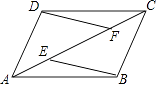
(1)求证:△ABE≌△CDF;
(2)连结DE,BF,求证:四边形DEBF是平行四边形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中, 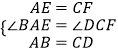 ,
,
∴△ABE≌△CDF(SAS)
(2)证明:连接DE、BF,如图所示:
由(1)得:△ABE≌△CDF,
∴BE=DF,
同理:DE=BF,
∴四边形DEBF是平行四边形.
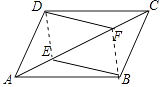
【解析】(1)由平行四边形的性质得出∠BAE=∠DCF,由SAS证明△ABE≌△CDF即可;(2)由全等三角形的性质得出BE=DF,同理:DE=BF,即可得出结论.
【考点精析】通过灵活运用平行四边形的判定与性质,掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+ax+b=0(b≠0)与x2+cx+d=0都有实数根,若这两个方程有且只有一个公共根,且ab=cd,则称它们互为“同根轮换方程”.如x2-x-6=0与x2-2x-3=0互为“同根轮换方程”.
(1)若关于x的方程x2+4x+m=0与x2-6x+n=0互为“同根轮换方程”,求m的值;
(2)已知方程①:x2+ax+b=0和方程②:x2+2ax+![]() b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数![]() 的图象经过点C,一次函数y=ax+b的图象经过点A、C
的图象经过点C,一次函数y=ax+b的图象经过点A、C
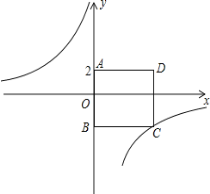
(1)求反比例函数和一次函数的解析式
(2)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
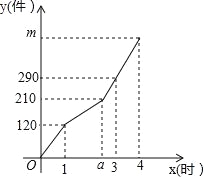
【题目】某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
(1)甲车间每小时生产产品 件,a= .
(2)求乙车间更换新设备之后y与x之间的函数关系式,并求m的值.
(3)若乙车间在开始更换新设备时,增加两名工作人员,这样可便更换设备时间减少0.5小时,并且更换后工作效率提高到原来的2倍,那么两个车间完成原任务量需几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
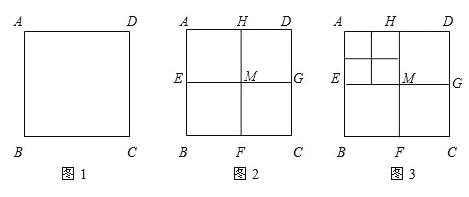
【题目】将正方形ABCD(如图1)作如下划分:
第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;
第2次划分:将图2左上角正方形AEMH再作划分,得图3,则图3中共有9个正方形;
(1)若每次都把左上角的正方形一次划分下去,则第100次划分后,图中共有______个正方形;
(2)继续划分下去,第几次划分后能有805个正方形?写出计算过程.
(3)能否将正方形性ABCD划分成有2018个正方形的图形?如果能,请算出是第几次划分,如果不能,需说明理由.
(4)如果设原正方形的边长为1,通过不断地分割该面积为1的正方形,并把数量关系和几何图形巧妙地结合起来,可以很容易得到一些计算结果,试着探究求出下面表达式的结果吧.
计算![]() .(直接写出答案即可)
.(直接写出答案即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com