
【题目】已知关于x的方程x2+ax+b=0(b≠0)与x2+cx+d=0都有实数根,若这两个方程有且只有一个公共根,且ab=cd,则称它们互为“同根轮换方程”.如x2-x-6=0与x2-2x-3=0互为“同根轮换方程”.
(1)若关于x的方程x2+4x+m=0与x2-6x+n=0互为“同根轮换方程”,求m的值;
(2)已知方程①:x2+ax+b=0和方程②:x2+2ax+![]() b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
b=0,p、q分别是方程①和方程②的实数根,且p≠q,b≠0.试问方程①和方程②是否能互为“同根轮换方程”?如果能,用含a的代数式分别表示p和q;如果不能,请说明理由.
【答案】(1)![]() ;(2)能,①
;(2)能,①![]() ,
,![]() ②
②![]() ,
,![]() ③
③![]() ,
,![]()
【解析】试题分析:(1)根据方程x2+4x+m=0与x2-6x+n=0互为“同根轮换方程”,得到m、n之间的关系为4m=-6n.然后设t是公共根,则有t2+4t+m=0,t2-6t+n=0,于是得到结论;(2)根据x2-x-6=0与x2-2x-3=0互为“同根轮换方程”,得到它们的公共根是3,从而得到当p=q=-3a时,有9a2-3a2+b=0.解得,b=-6a2.解得,p=-3a,x1=2a;q=-3a,x2=a,从而证得方程x2+ax+b=0(b≠0)与x2+2ax+![]() b=0互为“同根轮换方程”.
b=0互为“同根轮换方程”.
试题解析:(1)∵方程x2+4x+m=0与x26x+n=0互为“同根轮换方程”,
∴4m=6n.
设t是公共根,则有t2+4t+m=0,t26t+n=0.
解得,t=![]() .
.
∵4m=6n.∴t=![]() .
.
∴(![]() )2+4(
)2+4(![]() )+m=0.
)+m=0.
∴m=12.
(2)∵x2x6=0与x22x3=0互为“同根轮换方程”,
它们的公共根是3.
而3=(3)×(1)=3×(1).
又∵x2+x6=0与x2+2x3=0互为“同根轮换方程”。
它们的公共根是3.
而3=3×1.
∴当p=q=3a时,
有9a23a2+b=0.
解得:b=6a2.
∴x2+ax6a2=0,x2+2ax3a2=0.
解得:p=3a,x1=2a,q=3a,x2=a.
∵b≠0,
∴6a2≠0,
∴a≠0.
∴2a≠a.即x1≠x2.
又∵2a×![]() b=ab,
b=ab,
∴方程x2+ax+b=0(b≠0)与x2+2ax+12b=0能为“同根轮换方程”,p=q=3a.


科目:初中数学 来源: 题型:
【题目】列方程求解
(1)m为何值时,关于x的一元一次方程4x﹣2m=3x﹣1的解是x=2x﹣3m的解的2倍.
(2)已知|a﹣3|+(b+1)2=0,代数式![]() 的值比
的值比![]() b﹣a+m多1,求m的值.
b﹣a+m多1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点P从A点出发,按A→B→C的方向在AB和BC上移动.记PA=x,点D到直线PA的距离为y,则y关于x的函数关系的大致图像是( )
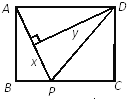
A.  B.
B. 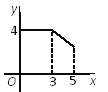 C.
C. 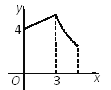 D.
D. 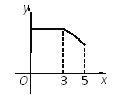
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;
![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=s时,以A、C、E、F为顶点四边形是平行四边形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F是ABCD对角线AC上两点,AE=CF. 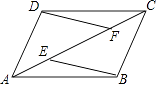
(1)求证:△ABE≌△CDF;
(2)连结DE,BF,求证:四边形DEBF是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com