【题目】计算：
（1）
﹣9 
+ 
（2）（ 
﹣ 
）÷ 
+ 
×2 ．
【答案】
（1）解：原式=2 
﹣3 +5 =4
（2）解：原式=（ 
﹣ 
）+2 
，
=（4﹣3）+6 
，
=1+6
【解析】（1）根据二次根式的运算性质结合二次根式的混合运算顺序，计算后即可得出结论；（2）根据二次根式的运算性质结合二次根式的混合运算顺序，计算后即可得出结论．
【考点精析】利用二次根式的性质与化简和二次根式的混合运算对题目进行判断即可得到答案，需要熟知1、如果被开方数是分数（包括小数）或分式，先利用商的算数平方根的性质把它写成分式的形式，然后利用分母有理化进行化简．2、如果被开方数是整数或整式，先将他们分解因数或因式，然后把能开得尽方的因数或因式开出来；二次根式的混合运算与实数中的运算顺序一样，先乘方，再乘除，最后加减，有括号的先算括号里的（或先去括号）．
科目：初中数学 来源： 题型：
【题目】阅读材料，解答问题．
例：若代数式
的值是常数2，则a的取值范围 2≤a≤4 ．
分析：原式=|a﹣2|+|a﹣4|，而|a|表示数x在数轴上的点到原点的距离，|a﹣2|表示数a在数轴上的点到数2的点的距离，所以我们可以借助数轴进行分析．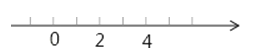
解：原式=|a﹣2|+|a﹣4|
在数轴上看，讨论a在数2表示的点左边；在数2表示的点和数4表示的点之间还是在数4表示的点右边，分析可得a的范围应是2≤a≤4．
（1）此例题的解答过程了用了哪些数学思想？请列举．
（2）化简
．
查看答案和解析>>
科目：初中数学 来源： 题型：
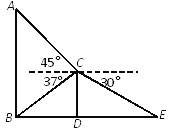
【题目】某班数学兴趣小组为了测量建筑物AB的高度，他们选取了地面上一点E，测得DE的长度为9米，并以建筑物CD的顶端点C为观测点，测得点A的仰角为45°，点B的俯角为37°，点E的俯角为30°．
（1）求建筑物CD的高度；
（2）求建筑物AB的高度．
(结果精确到0.1米，参考数据：
≈1.73，sin37°≈
，tan37°≈
)
查看答案和解析>>
科目：初中数学 来源： 题型：
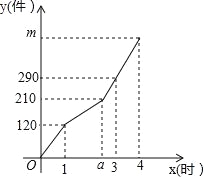
【题目】某工厂甲、乙两个车间同时开始生产某种产品，产品总任务量为m件，开始甲、乙两个车间工作效率相同．乙车间在生产一段时间后，停止生产，更换新设备，之后工作效率提高．甲车间始终按原工作效率生产．甲、乙两车间生产的产品总件数y与甲的生产时间x（时）的函数图象如图所示．
（1）甲车间每小时生产产品 件，a= ．
（2）求乙车间更换新设备之后y与x之间的函数关系式，并求m的值．
（3）若乙车间在开始更换新设备时，增加两名工作人员，这样可便更换设备时间减少0.5小时，并且更换后工作效率提高到原来的2倍，那么两个车间完成原任务量需几小时？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，一次函数y=ax+b的图象与x轴相交于点A（-2，0），与y轴交于点C，与反比例函数
在第一象限内的图象交于点B（m，n），连结OB．若S△AOB=6，S△BOC=2．
（1）求一次函数的表达式；
（2）求反比例函数的表达式．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com