
【题目】某文具店销售甲、乙两种圆规,当销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元.
(1)问该文具店销售甲、乙两种圆规,每只的利润分别是多少元?
(2)在(1)中,文具店共销售甲、乙两种圆规50只,其中甲种圆规为a只,求文具店所获得利润P与a的函数关系式,并求当a≥30时P的最大值.
【答案】(1)甲种圆规每只的利润是4元,乙种圆规每只的利润是5元;(2)220.
【解析】试题分析:(1)设文具店销售甲、乙两种圆规,每只的利润分别是x元、y元,根据题意“销售5只甲种、1只乙种圆规,可获利润25元,销售6只甲种、3只乙种圆规,可获利润39元”,列出的方程组,解方程组即可;(2)根据题意可以列出文具店所获利p与a的函数关系式,然后根据当a≥30,可以求得p的最大值即可.
试题解析:
(1)设文具店销售甲、乙两种圆规,每只的利润分别是x元、y元,得,
![]() ,
,
解得:![]() ,
,
即文具店销售甲种圆规每只的利润是4元,乙种圆规每只的利润是5元;
(2)由题意可得,p=4a+5(50﹣a)=4a+250﹣5a=250﹣a,
∵a≥30,
∴当a=30时,p取得最大值,
此时,p=250﹣30=220,
即文具店所获利p与a的函数关系式是p=250﹣a,当a≥30时p的最大值是220.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
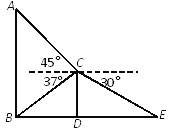
【题目】某班数学兴趣小组为了测量建筑物AB的高度,他们选取了地面上一点E,测得DE的长度为9米,并以建筑物CD的顶端点C为观测点,测得点A的仰角为45°,点B的俯角为37°,点E的俯角为30°.
(1)求建筑物CD的高度;
(2)求建筑物AB的高度.
(结果精确到0.1米,参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
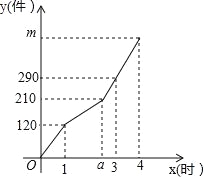
【题目】某工厂甲、乙两个车间同时开始生产某种产品,产品总任务量为m件,开始甲、乙两个车间工作效率相同.乙车间在生产一段时间后,停止生产,更换新设备,之后工作效率提高.甲车间始终按原工作效率生产.甲、乙两车间生产的产品总件数y与甲的生产时间x(时)的函数图象如图所示.
(1)甲车间每小时生产产品 件,a= .
(2)求乙车间更换新设备之后y与x之间的函数关系式,并求m的值.
(3)若乙车间在开始更换新设备时,增加两名工作人员,这样可便更换设备时间减少0.5小时,并且更换后工作效率提高到原来的2倍,那么两个车间完成原任务量需几小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与x轴相交于点A(-2,0),与y轴交于点C,与反比例函数![]() 在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
(1)求一次函数的表达式;
(2)求反比例函数的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
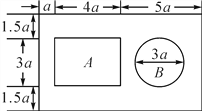
【题目】某居民小区响应党的号召,开展全民健身活动.该小区准备修建一座健身馆,其设计方案如图所示,A区为成年人活动场所,B区为未成年人活动场所,其余地方均种花草.(π取3.14)
(1)活动场所和花草的面积各是多少?
(2)整座健身馆的面积是成年人活动场所面积的多少倍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com